杂七杂八的练习（2）

一、接雨水问题

1、问题描述

输入N个非负整数，可以表示成一个若干个方块堆积的图，图中每一列的宽度均为1，高度为输入的数字，请计算在下雨时，该图能容纳多少面积的雨水。例如：输入[0,1,0,2,1,0,1,3,2,1,2,1]，如下图所示，则输出为6。

输入描述：

输入为两行，第一行为N，代表非负整数的个数，第二行为N个非负整数。

2、算法思路

算法从第一层开始计数，将每层积累的雨水数累加起来。

引入两个变量l、r，表示读取到的最邻近的两堵墙的位置；从左到右依次读取，当读取到新的墙时，更新l、r，并通过r-l得到两堵墙之间的雨水数，将其累加得到最终结果。

3、代码实现

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;


int main() {
	int n,h=0;
	cin>>n;
	int A[n];
	for(int i=0;i<n;i++){
		cin>>A[i];
		if(h<A[i])h=A[i];//得到最高高度
	}
	int x=0;
	for(int i=0;i<h;i++){
		int l=-1,r=-1;//初始化l、r
		for(int j=0;j<n;j++){
			if((A[j]>=i+1)){
        l=r;
				r=j;//更新
				if(r>=0 && l>=0){
					x+=(r-l-1);//累加
				}
			}
		}
	}
	cout<<x;
	return 0;
}

二、单调上升序列

1、问题描述

给定一长度为n的数列，请在不改变原数列顺序的前提下，从中随机的取出一定数量的整数，并使这些整数构成单调上升序列。输出这类单调上升序列的最大长度。

输入格式：

第一行，一正整数n，表示数列的长度第二行，n个数，表示数列

输出格式：

一行，一个整数。

输入样例：

5 3 1 5 4 2

输出样例：

2、算法思路

这类题目需要在一个序列中不连续地找到子序列，让其满足一定的要求。在数据容量不大的情况下，可以使用全局变量+函数调用的方式进行遍历，具体实现方法如下面代码，在每一个函数中展开多个子函数直到达到终止条件。

3、代码实现

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

int max1=0;
int n;
int num[1000];

void fun(int i,int o){//函数输入：当前数列的最后一个数i，序列长度o
	if(o>max1){
		max1=o;
	}//更新max1
	for(int k=i+1;k<n;k++){//包含函数终止条件
		if(num[k]>num[i])
			fun(k,o+1);//若找到比i大的数，进入子函数
	}
	return;
}

int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>num[i];
	}
	for(int i=0;i<n;i++){
		fun(i,1);
	}
	cout<<max1;
}

三、兔子的公共祖先

1、问题描述

小红养了一些很可爱的兔子。有一天，她突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行繁衍：一对兔子从出生后第二个月起，每个月刚开始的时候都会产下一对小兔子。我们假定，在整个过程中兔子不会出现任何意外。小红把兔子按出生顺序，把兔子们从1开始标号，并且小红的兔子都是 1 号兔子和 1 号兔子的后代。如果某两对兔子是同时出生的，那么小红会将父母标号更小的一对优先标号。

如果我们把这种关系用图画下来，前六个月大概就是这样的：

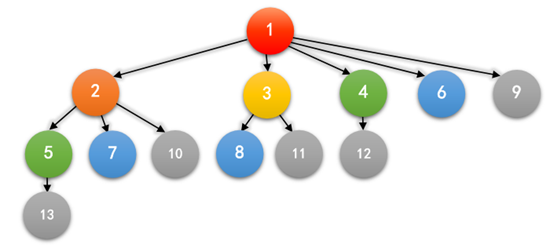
其中，一个箭头 A → B 表示 A 是 B 的祖先，相同的颜色表示同一个月出生的兔子。

为了更细致地了解兔子们是如何繁衍的，有一个问题：她想知道关于每两对兔子ai和bi，他们的最近公共祖先是谁。

一对兔子的祖先是这对兔子以及他们父母（如果有的话）的祖先，而最近公共祖先是指两对兔子所共有的祖先中，离他们的距离之和最近的一对兔子。比如，5 和 7 的最近公共祖先是 2，1 和 2 的最近公共祖先是 1，6 和 6 的最近公共祖先是 6。

输入格式：

一行包含 2 个正整数，表示a和b。

输出格式：

答案，一个正整数。

输入样例：

2 3

输出样例：

2、算法思路

首先观察其数学模型，我们可以看到每个月出生的兔子的对数满足斐波那契数列，从2号兔子开始算起，每一个月出生的兔子对数为：1、1、2、3、5、8……

而且，当月出生的兔子的祖先从1递增，如：6~8号兔子是同一个月出生的，它们的祖先依次为1、2、3；9~13号兔子是同一个月出生的，它们的祖先依次为1、2、3、4、5。

以此，我们可以构建一个数组rabbit[]，用以存储每一只兔子的双亲，我们需要判断的即为rabbit[a]与rabbit[b]的共同祖先。

对于rabbit[a]与rabbit[b]的共同祖先，我们可以以如下方法判断：

当rabbit[a]==rabbit[b]，找到共同祖先。
当rabbit[a]==b或rabbit[b]==a，找到共同祖先。
如果不满足上述两种情况，当rabbit[a]<rabbit[b]，则取b=rabbit[b]，（更新较大的rabbit），并继续比较；反之也相同。

3、代码实现

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

int main(){
	int a,b;
	cin>>a>>b;
	if(a==b){
		cout<<a;
		return 0;
	}//特殊情况
	int num[100],rab[1000];
	num[0]=1;
	num[1]=1;
	int i=2;
	while(i){
		num[i]=num[i-1]+num[i-2];
		if(num[i]>a && num[i]>b)break;
		i++;
	}//构造斐波那契数列
	int x=0;
	for(int j=0;j<i;j++){
		for(int k=0;k<num[j];k++){
			rab[x]=k+1;
			x++;
		}
	}//构造rabbit数组
	int A=a-2,B=b-2;
	while(1){
		if(rab[A]==rab[B]){
			cout<<rab[A];
			break;
		}
		else if(A==rab[B]-2){
			cout<<A+2;
			break;
		}
		else if(B==rab[A]-2){
			cout<<B+2;
			break;
		}
		else{
			if(rab[A]<rab[B]){
				B=rab[B];
			}
			else A=rab[A];
		}
	}//判断
}

四、重复的DNA序列

1、问题描述

所有 DNA 都由一系列缩写为 A，C，G 和 T 的核苷酸组成，如：“ACGAATTCCG”。编写一个函数来查找 DNA 分子中所有出现超过一次的 10 个字母长的序列（子串）。

输入格式：

一行DNA序列。

输出格式：

所有重复的子串。

输入样例：

AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT

输出样例：

AAAAACCCCC CCCCCAAAAA

2、算法思路

最简单的算法为从头读取10位长的字符串，并将每个子串与该子串位置后面的字符串比较，将符合结果的字符串输出。

问题的另一个难点为输出顺序，测例中的输出顺序是根据字典排序的，所以我们需要将符合结果的字符串先存储起来，最后再根据字典排序输出。这里可以用set进行自动的排序。

3、代码实现

#include <iostream>
#include <string>
#include <set>
#include <string>
#include <algorithm>

using namespace std;

set<string> S;//容器

void com(string str,int i){
	for(int k=i+1;k<str.size()-10;k++){
		string t=str.substr(k,10);
		string s=str.substr(i,10);
		if(s==t){
			S.insert(s);//满足条件，插入
			return;
		}
	}
}

int main() {
	string str;
	cin>>str;
	for(int i=0;i<str.size()-10;i++){
		com(str,i);
	}	
	for(set<string>::iterator it=S.begin();it!=S.end();it++)
 		cout<<*it<<endl;//迭代器遍历
}

五、索引处的解码字符串

1、问题描述

给定一个编码字符串 S。为了找出解码字符串并将其写入磁带，从编码字符串中每次读取一个字符，并采取以下步骤：

如果所读的字符是字母，则将该字母写在磁带上。

如果所读的字符是数字（例如 d），则整个当前磁带总共会被重复写 d-1 次。

现在，对于给定的编码字符串 S 和索引 K，查找并返回解码字符串中的第 K 个字母。

输入格式：

两行，第一行为编码的字符串，第二行为K

输出格式：

解码后的第K个字母。

输入样例：

leet2code3 10

输出样例：

解释：

解码后的字符串为 “leetleetcodeleetleetcodeleetleetcode”。字符串中的第 10 个字母是 “o”。

2、算法思路

依次读取原字符串str的每一位，解码得出结果字符串code，将其输出即可。

将字符串中的连续数字转换为整型的框架如下：

	int num=0;		
	if(str[i]<='9' && str[i] >= '0'){
		num*=10;
		num+=(str[i]-'0');
	}

但是，检查测例中出现了一种特殊情况：a2445657646，且输出的为第1个字母。如果将此字符串解码，无疑会发生越界。那么，我们只能在解码时增加一点限制条件，让其不发生越界，且满足其他测例的解码要求。（我使用的方法是限制转换得到的数字的大小，让数字大小的上界不超过某一个较大的数，这样可以保证不发生越界，且满足其他测例）

3、代码实现

#include <iostream>
#include <string>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;

int main() {
	string str,code;
	cin>>str;
	int n;
	cin>>n;
	int num=0;
	for(int i=0;i<=str.size();i++){
		if(str[i]<='9' && str[i] >= '0'){
			if(num>n*100){
				break;
			}//限制大小
			num*=10;
			num+=(str[i]-'0');
		}
		else {
			if(num){
				string code0=code;
				for(int j=0;j<num-1;j++){
					code+=code0;
				}
				num=0;
			}
			code+=str[i];
		}
	} 
	cout<<code[n-1];
}

六、拼数

1、问题描述

设有n个正整数，将它们联接成一排，组成一个最大的多位整数。输入格式第一行，一个正整数n。第二行，n个正整数。输出格式一个正整数，表示最大的整数

输入样例：

3 13 312 343

输出样例：

34331213

2、算法思路

本质上是把输入的数组进行排序，排序后依次输出。

一开始的思路是每次都从最高位开始比较，后来细化了一下思路，发现将每个数字作为字符串进行处理时最为简单的，我自己实现的思路为：依次比较字符串的每一位（从第0位开始），将比较结果较小的调至后面。

int s=num[i].size()>num[j].size()?num[j].size():num[i].size();
for(int k=0;k<s;k++)
{
	if(num[i][k]>num[j][k])
	{
		break;
	}
	else if(num[i][k]<num[j][k])
	{
  	string t=num[i];
  	num[i] = num[j];
  	num[j] = t;
	}
}

答案使用了更加简单的方法实现比较，对字符串A、B，直接比较A+B>A-B是否成立（由于是string类型，可以直接比较），根据比较结果排序即可。

3、代码实现

#include<bits/stdc++.h> 
using namespace std;
string a[30]; //使用string更方便一些(可以直接比较大小)
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i]; //读入
    for(int i=1;i<n;i++) //排序
    {
        for(int j=i+1;j<=n;j++)
        {
            if(a[j]+a[i]>a[i]+a[j]) //string类型可以直接比较大小
            {
                swap(a[j],a[i]);  //交换a[i]与a[j],同样可以用swap(a[i],a[j]);
                /*
                    举个例子:如果是12,34，由于3412>1234，所以肯定要交换一下，直接用swap就可以了
                */
            }
        }
    } //排序结束
    for(int i=1;i<=n;i++) cout<<a[i]; //由于已经排好序了，直接输出即可
    return 0;
}

七、按要求处理数字

1、问题描述

给定一个数列，对于其中重复的数字，只保留一个，把其余相同的数去掉，然后再把这些数从小到大排序

输入格式：

第1行为一个正整数N，表示了数列长度。第2行包含N个非负整数。

输出格式：

共2行，第一行为处理后数列的长度，第二行为数字以空格隔开的处理后数列。

输入样例 :

3 2 1 1

输出样例 :

2 1 2

2、算法思路

把这道题写进来是为了熟悉STL的用法。

为了得到顺序、不重复的序列，第一个想法就是使用set容器。将输入的数字一个一个加入set中，然后直接利用迭代器输出即可。

3、代码实现

#include<iostream>
#include<set>

using namespace std;

int main(){
	int n;
	cin >> n;
	set<int> s;
	for(int i=0;i<n;i++){
		int t;
		cin>>t;
		s.insert(t);
	}
	cout<<s.size()<<endl;
	for(set<int>::iterator it=s.begin();it != s.end();it++){
		cout<<*it<<" ";
	}
	/*
	另一种输出方式
  while(!s.empty())
  {
  	cout<<*s.begin()<<" ";           
  	s.erase(s.begin()); 
  }
	*/
}

八、切木板

1、问题描述

小明想要亲自修复在他的一个小牧场周围的围栏。他测量栅栏并发现他需要N根木板，每根的长度为整数Li。于是，他神奇地买了一根足够长的木板，长度为所需的N根木板的长度的总和，他决定将这根木板切成所需的N根木板。（小明在切割木板时不会产生木屑，不需考虑切割时损耗的长度)小明切割木板时使用的是一种特殊的方式，这种方式在将一根长度为x的模板切为两根时，需要消耗x个单位的能量。小明拥有无尽的能量，但现在提倡节约能量，所以作为榜样，他决定尽可能节约能量。显然，总共需要切割N-1次，问题是，每次应该怎么切呢？请编程计算最少需要消耗的能量总和。

输入格式：

第一行: 整数N，表示所需木板的数量；

第2到N+1行: 每行为一个整数，表示一块木板的长度；

输出格式：

一个整数，表示最少需要消耗的能量总和。

输入样例：

3 8 5 8

输出样例：

2、算法思路

首先，先将木板按从小到大的顺序排列，由于木板长度可重复，我们可以使用multiset实现。

经过举例并进行验证，发现最快的方式为每一步都进行二分，如果当前木板恰有奇数个，则切木板的位置偏向较大的一边，例如：

2 4 7 8 9

2 4 7

8 9

2 4

7 8

为了实现二分，我们使用递归来实现，并引入一个长度为N的数组num，用来记录第i块木板被切了多少次，最终结果为：

$result = \sum^{n-1}_{i=0}num[i]\times length_i$

3、代码实现

#include<iostream>
#include<set>

using namespace std;

void fun(int *num,int l,int r){//num为辅助数组，l、r为起止点（包括r）
	int n=r-l+1；//当前需要分的木板长度
	if(n==1)return; //长度为一，返回
	for(int i=l;i<=r;i++){
		num[i]++;//将当前的木板次数均+1
	}
	int mid;//取中点，根据奇偶区分
	if(n%2==0){
		mid = l+n/2;
	}
	else{
		mid = l+n/2+1;
	}
	fun(num,l,mid-1);//递归左边
	fun(num,mid,r);//递归右边
}

int main(){
	int n;
	cin >> n;
	multiset<int> s;
	int num[n];//辅助数组
	for(int i=0;i<n;i++){
		int t;
		cin>>t;
		s.insert(t);
		num[i]=0;//初始化
	}
	fun(num,0,n-1);//二分计算
	int max=0,i=0;
	multiset<int>::iterator it=s.begin();
	for(;it != s.end();it++){
		max+=num[i]*(*it);
        i++;
	}
	cout<<max;
}

九、火星人

1、问题描述

人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言，但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的，首先，火星人把一个非常大的数字告诉人类科学家，科学家破解这个数字的含义后，再把一个很小的数字加到这个大数上面，把结果告诉火星人，作为人类的回答。

火星人用一种非常简单的方式来表示数字――掰手指。火星人只有一只手，但这只手上有成千上万的手指，这些手指排成一列，分别编号为1,2,3…。火星人的任意两根手指都能随意交换位置，他们就是通过这方法计数的。

一个火星人用一个人类的手演示了如何用手指计数。如果把五根手指――拇指、食指、中指、无名指和小指分别编号为1,2,3,4和5，当它们按正常顺序排列时，形成了5位数12345，当你交换无名指和小指的位置时，会形成5位数12354，当你把五个手指的顺序完全颠倒时，会形成54321，在所有能够形成的120个5位数中，12345最小，它表示1；12354第二小，它表示2；54321最大，它表示120。下表展示了只有3根手指时能够形成的6个3位数和它们代表的数字：

三进制数

123 132 213 231 312 321

代表的数字

1 2 3 4 5 6

现在你有幸成为了第一个和火星人交流的地球人。一个火星人会让你看他的手指，科学家会告诉你要加上去的很小的数。你的任务是，把火星人用手指表示的数与科学家告诉你的数相加，并根据相加的结果改变火星人手指的排列顺序。输入数据保证这个结果不会超出火星人手指能表示的范围。

输入格式：

第一行一个正整数N，表示火星人手指的数目。第二行是一个正整数M，表示要加上去的小整数。下一行是1到N这N个整数的一个排列，用空格隔开，表示火星人手指的排列顺序。

输出格式：

N个整数，表示改变后的火星人手指的排列顺序。每两个相邻的数中间用一个空格分开，不能有多余的空格。

输入样例 :

5 3 1 2 3 4 5

输出样例 :

1 2 4 5 3

2、算法思路

题目有点长，不过题意简单来说就是求出当前给出的全排列的第下m个全排列。

可以直接使用离散数学学过的求不重复全排列的算法实现，代码实现也不困难，需要找到两个位置j、p，j是第一个需要调换的位置，p为j后面可以与之调换的位置。调换后将j后面的数字从小到大排序即可。

3、代码实现

#include<iostream>
#include<set>

using namespace std;

int main(){
	int n,m;
	cin >> n >> m;
	int num[n];
	for(int i=0;i<n;i++){
		int t;
		cin>>t;
		num[i]=t;
	}
	for(int i=0;i<m;i++){//开始计算全排列
		int j=n-2;
		for(;j>=0;j--){
			if(num[j]<num[j+1])break;
		}//找到位置j
		int p=n-1;
		for(;p>=0;p--){
			if(num[j]<num[p])break;
		}//找到位置p，将j、p交换
		int temp=num[p];
		num[p] = num[j];
		num[j] = temp;
		j++;
		k=n-1;
		while((j<k))//把后面的逆序，相当于从小到大排序 
     {
       t=b[j];  
       b[j]=b[k];
       b[k]=t;
       j++;
       k--;
     }
	}
	for(int i=0;i<n;i++){
		cout << num[i] <<" ";
	}
}

十、最短电文

1、问题描述

对于一份英文电文，我们可以通过二进制前缀编码（Huffman Coding），将其变为只含“01”的二进制序列。现假设该电文只含小写英文字母（a-z），且至少包含两个不同的字符。要求我们求出该电文经过编码后的长度。

输入样例 :

ssuuusuluu

输出样例 :

2、算法思路

构造哈夫曼树实现即可，不过构造之后需要依次读取字符结点的父结点，得到编码长度再做计算。

哈夫曼树的结点结构如下：

class TreeNode{
	public:
		int anc;//编码长度
		int al;//对应哪个字母
		int weight;
		int par;
		int lc,rc;
		TreeNode(){
			par=lc=rc=-1;
			weight=0;
			al=-1;
			anc=0;
		}
};

3、代码实现

#include <iostream>
#include <stack>
#include <cstring>
using namespace std;

class TreeNode{
	public:
		int anc;
		int al;
		int weight;
		int par;
		int lc,rc;
		TreeNode(){
			par=lc=rc=-1;
			weight=0;
			al=-1;
			anc=0;
		}
};

int main(){
	string str;
	cin >> str;
	int alg[26] = {0};
	for(int i=0 ; i<str.size();i++){
		alg[str[i]-'a']++;
	}
	int num=0;
	for(int i=0 ; i<26;i++){
		if(alg[i] > 0)num++;
	}
	TreeNode t[2*num-1];
	int j=0;
	for(int i=0 ; i<26;i++){
		if(alg[i] > 0){
			t[j].al=i;
			t[j].weight = alg[i];
			j++;
		}
	}
	for(int i=num ; i<2*num-1;i++){
		int min1=999,min2=999,min1_ind=0,min2_ind=0;
		for(int j=0;j<i;j++){//find min1
			if(t[j].par == -1 && t[j].weight < min1){
				min1 = t[j].weight;
				min1_ind = j;
			}
		}
		for(int j=0;j<i;j++){//find min2
			if(t[j].par == -1 && j != min1_ind && t[j].weight < min2){
				min2 = t[j].weight;
				min2_ind = j;
			}
		}
		t[i].weight = min1+min2;
		t[i].lc = min1_ind;
		t[i].rc = min2_ind;
		t[min1_ind].par = t[min2_ind].par = i;
		//构造新结点
	}
	int res=0;
	for(int i=0;i<num;i++){
		int k=i;
		while(t[k].par != -1){
			k=t[k].par;
			t[i].anc++;
			//计算编码长度
		}
		res+=(t[i].anc*t[i].weight);//计算结果
	}
	cout<<res<<endl;
    return 0;
}

一、接雨水问题

1、问题描述

2、算法思路

3、代码实现

二、单调上升序列

1、问题描述

2、算法思路

3、代码实现

三、兔子的公共祖先

1、问题描述

2、算法思路

3、代码实现

四、重复的DNA序列

1、问题描述

2、算法思路

3、代码实现

五、索引处的解码字符串

1、问题描述

2、算法思路

3、代码实现

六、拼数

1、问题描述

2、算法思路

3、代码实现

七、按要求处理数字

1、问题描述

2、算法思路

3、代码实现

八、切木板

1、问题描述

2、算法思路

3、代码实现

九、火星人

1、问题描述

2、算法思路

3、代码实现

十、最短电文

1、问题描述

2、算法思路

3、代码实现

CATALOG

FEATURED TAGS

FRIENDS