栈
一、Ackerman函数
Ackerman函数有$A(n,m)$有两个独立的整变量$m\ge0,n\ge0$,其定义如下
$A(1,0)=2$
$A(0,m)=1 ,m\ge0$
$A(n,0)=n+2, n\ge2$
$A(n,m)=A(A(n-1,m),m-1), n\ge1且m\ge1$
根据定义式可以简单地写出它的递归代码:
int Ackerman(int n,int m){
if(n<0 || m<0)return -1; //无定义
if(n==1 && m==0)return 2;
if(n==0)return 1;
if(m==0)return n+2;
return Ackerman(Ackerman(n-1,m),m-1);
}
字符串
一、子串定位:KMP算法
1、算法思路
定义主串串为目标串S,子串为模式串P。在朴素模式匹配算法中,每次匹配不成功之后,模式串只是向后移动1位,即存在大量回溯;我们可以利用部分匹配的结果,让模式串在不匹配时可以往后移动尽量远的距离,减少匹配次数。
KMP算法只针对模式串进行分析,对模式串求出数组Next[j],在模式串第j位比较失败之后利用Next[j]得到往后移几位。
Next数组的实质是找模式串中的最长相同的前缀和后缀(前缀不包括最后一个字符,后缀不包括第一个字符),实际意义为k=模式串第j位前的子串最长相同的前缀和后缀的长度+1,即将子串移动至第k位再次进行比较,如图所示。
 \(Next[j] =\begin{cases}
0, j=1时 \\
Max \{ k | 1<k<j \ and\ p_1p_2…p_{k-1}= p_{j-k+1}…p_{j-1} \} \\
1,其它情况
\end{cases}\)
\(Next[j] =\begin{cases}
0, j=1时 \\
Max \{ k | 1<k<j \ and\ p_1p_2…p_{k-1}= p_{j-k+1}…p_{j-1} \} \\
1,其它情况
\end{cases}\)
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| S | a | b | a | c | a | b | c |
| Next[j] | 0 | 1 | 1 | 2 | 1 | 2 | 3 |
| NextVal[j] | 0 | 1 | 0 | 2 | 0 | 1 | 3 |
根据上式,假设我们已经求出了next[j]数组,再将下标j按照C++的规则从0开始,就可以得到KMP算法的基本代码:
int KMP(string s,string t){
int i=0,j=0;
int n=s.size(),m=t.size();
while(i<n && j<m){
if(j==-1 || s[i]==t[j]){
i++;
j++;
}
else{
j=next[j];
}
}
if(j==m)return i-j;
else return -1;
}
2、Next数组
我们的代码依赖了数组next[j],next数组的定义上面已经说明,但它的求法更加精妙,首先我们贴出它的代码:
/*
这个算法得出的next[i]为最长前后缀的长度,即代表最长前缀的下一个字符的位置
*/
void getNext(string s){
next[0]=-1;
next[1]=0;
int i=2;//i代表填充next数组的i位置
int cn=0;//cn始终代表字符串i-1位置前面的字符串的最长前缀的下一个字符的位置
while (i<s.size()){
if(s[i-1]==s[cn])//如果字符串i-1位置上的字符等于字符串cn位置上的字符的话,直接在next[i]的基础上加1即可
next[i++]=++cn;
else if(cn>0)//这个条件满足,说明可以往前跳,让cn往前跳
cn=next[cn];
else
next[i++]=0;//字符串i位置前面的字符串没有前缀
}
}
以abacabc为例:
- next[0]=-1
- next[1]=0
- i=2,cn=0,s[1]!=s[0],且cn==0,next[2]=0
- i=3,cn=0,s[2]==s[0],next[3]=++cn=1
- i=4,cn=1,s[3]!=s[1],且cn>0,cn=next[1]=0,重复一次循环,i=4,cn=0,s[3]!=s[0],next[4]=0
- i=5,cn=0,s[4]==s[0],next[4]=++cn=1
- i=6,cn=0,s[5]==s[0],next[5]=++cn=2
比较难理解的为cn=next[cn]这段代码,实际为将当前前缀长度跳回到cn这一字符的最长前缀,由于next[cn]的前后缀必相同,只需继续再次比较cn与i-1的字符即可,如图:
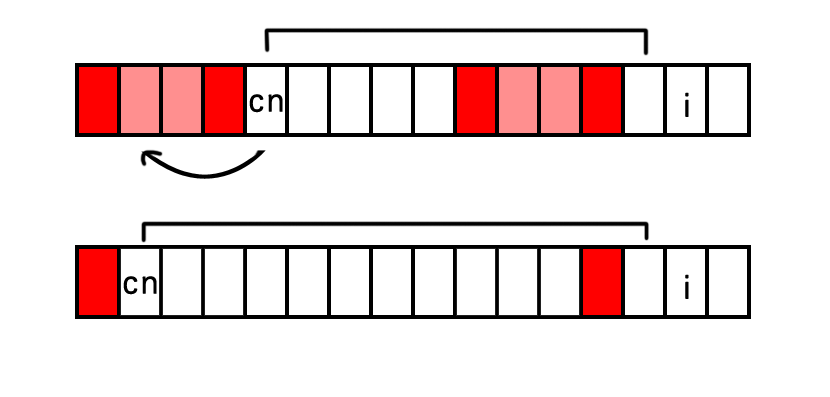
3、NextVal数组
观察s[4],当它不匹配时,按照next行回溯到s[1]也为字母a,这时再匹配a是徒劳的,因为已知a不匹配,所以就继续退回到s[1]字母a的next[1]=0。为了进行优化,就有了nextval:
若要求nextval[i],将next[i]的值对应的位的值与i的值进行比较: 若相等,nextval[i]=nextval[ next[i] ]; 若不相等,则nextval[i]=next[i]。
代码如下:
int get_nextval(string T){
//求模式串T的next函数修正值并存入数组nextval。
for(int i=1;i<T.size();i++){
if(T[next[i]] == T[i])
nextval[i]=nextval[next[i]];
else nextval[i]=next[i];
}
}//get_nextval
数组
一、快速转置算法
1、稀疏矩阵的三元组存储
矩阵本身的数据:行、列、元素个数
矩阵元素的数据:行序号、列序号、元素值
struct Triple{
int I,j;
elementtype e;
}; //矩阵元素
struct TSMatrix{
Triple data[Max+1];
int mu,nu,tu;
}; //矩阵
而由于稀疏矩阵的数据排列是行对齐的(根据行的顺序排列),所以如果进行转置,需要重新对数据进行排列,快速转置则是在尽可能少次数地遍历矩阵的情况下完成转置。
2、算法思路
首先我们给出一个$5\times5$的稀疏矩阵:
| 数组data | 5/行 | 5/列 | 6/元素个数 |
|---|---|---|---|
| 0 | 1 | 1 | 3 |
| 1 | 1 | 5 | 7 |
| 2 | 2 | 3 | -1 |
| 3 | 3 | 1 | -1 |
| 4 | 3 | 2 | -2 |
| 5 | 5 | 4 | 2 |
经过转置后,它的排列需要是这样:
| 数组data | 5/行 | 5/列 | 6/元素个数 |
|---|---|---|---|
| 0 | 1 | 1 | 3 |
| 1 | 1 | 3 | -1 |
| 2 | 2 | 3 | -2 |
| 3 | 3 | 2 | -1 |
| 4 | 4 | 5 | 2 |
| 5 | 5 | 1 | 7 |
为了预先确定矩阵M中的每一列的第一个非零元素在数组中的位置,需要先求得矩阵M中的每一列中非零元素的个数。为此,需要设置两个一维数组num[n]和cpot[n],其中n为矩阵列数。
-
num[]:储存每一列非零元素的个数
-
cpot[]:储存每一列的第一个非零元素在数组中的位置
通过这两个数组,我们可以在仅遍历数组两次的情况下完成矩阵的转置:
- 在第一次遍历时,通过对列的遍历,我们可以得到num[]。
- cpot[1]=0 cpot[col]=cpot[col-1]+num[col-1]
- 第二次遍历即可根据cpot开始元素的转置:每读取一个元素,若列为i,则将行列调换,放入新的data[cpot[data[i].j]]]之中,并将cpot[i]+1。
- 完成第二次遍历,完成算法。
3、代码实现
TSMatrix trans(TSMatrix mat){
TSMatrix nmat;
nmat.mu=mat.nu;
nmat.nu=mat.mu;
nmat.tu=mat.tu;
int num[10]={0};
int cpot[mat.nu];
for(int i=0;i<mat.tu;i++){
num[mat.data[i].j]++;
}
cpot[0]=0;
for(int i=1;i<mat.nu;i++){
cpot[i]=cpot[i-1]+num[i-1];
}
for(int i=0;i<mat.tu;i++){
nmat.data[cpot[mat.data[i].j]].I=mat.data[i].j;
nmat.data[cpot[mat.data[i].j]].j=mat.data[i].I;
nmat.data[cpot[mat.data[i].j]].e=mat.data[i].e;
cpot[mat.data[i].j]++;
}
return nmat;
}
二、求杨辉三角系数
1、数学模型
杨辉三角是二项式系数在三角形中的一种几何排列,即我们熟知的二项式系数$(a+b)^n=C^0_na^n+C^1_na^{n-1}b^1+\dots+C^n_nb^n$中的$C^k_n$。

如图,对于n次二项式,设第一行为n=0的系数,则n次二项式共有n+1个系数,设为0~n。
那么,我们可以发现,对于每一个n,$a_n[0]=a_n[n]=1$,且对于$0<k<n$,$a_n[k]=a_{n-1}[k-1]+a_{n-1}[k]$。
2、代码实现
这样一来,建立一个数组进行递归计算,可以简单的求出n次二项式的二次项系数。
void coff(int *a,int n){ //arr的大小为n+1
if(n==1){
a[0]=a[1]=1;
}
else{
coff(a,n-1);
a[n]=1;
for(int i=n-1;i>0;i--){ //从最后一个开始,可以直接修改数组内容且不影响计算
a[i]=a[i]+a[i-1];
}
}
}
3、测试函数
#define N 10
int arr[N+1];
int main()
{
coff(arr,N);
for(int i=0;i<=N;i++){
cout<<arr[i]<<endl;
}
return 0;
}