C++ 数据结构 算法

数据结构：图结构

数据结构课程笔记

 Max.C     2019-12-29   15664 words    & views

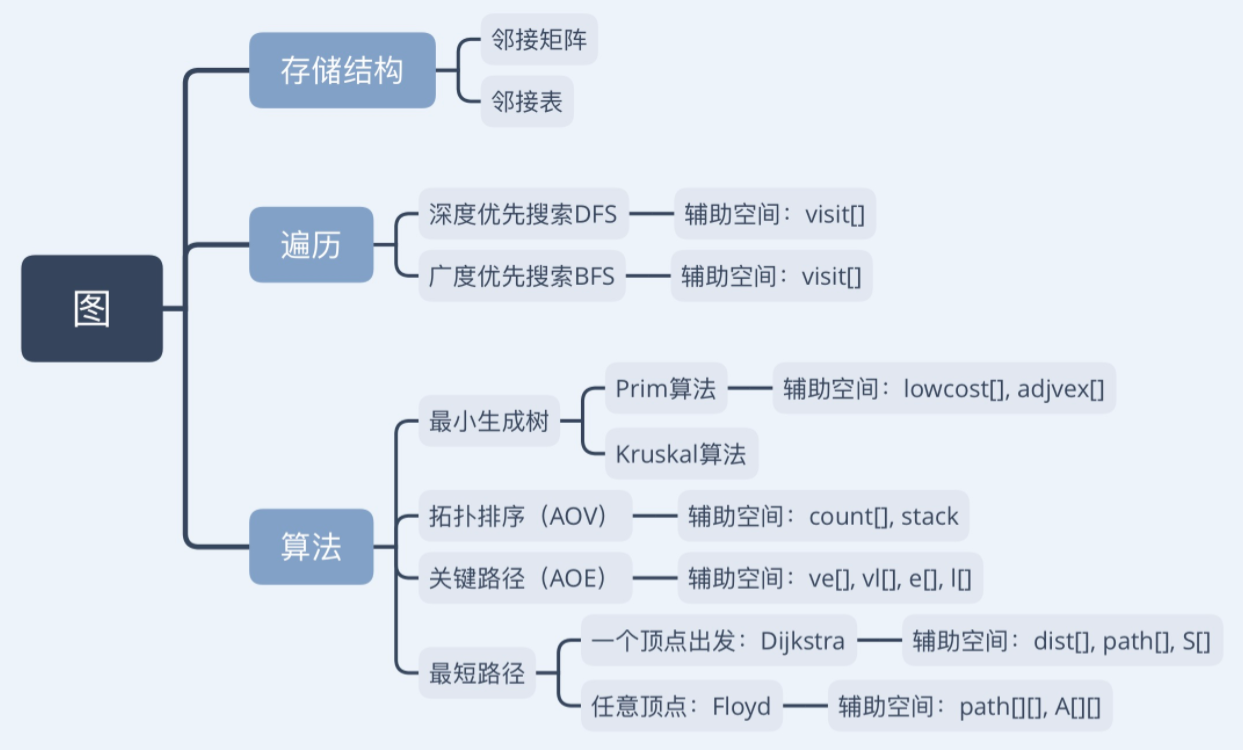
图

一、存储设计

1、邻接矩阵

设图 G = (V, E)是一个有 n 个顶点的图，则图的邻接矩阵$G.arcs[n][n]$定义为：

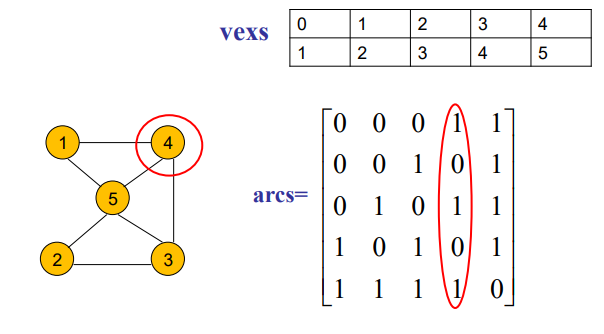
\[G.arcs[i][j]=\begin{cases} 1 &若(v_i, v_j)∈E \\ 0 & else \end{cases}\]

无向图的邻接矩阵是对称的，在无向图中，第 i 行/列 1 的个数就是顶点i的度。

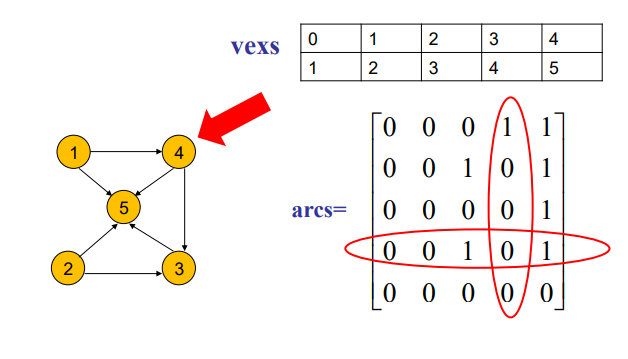
有向图的邻接矩阵可能是不对称的，在有向图中，每个1对应的行为起点i，对应的列为终点j，第 i 行 1 的个数就是顶点 i 的出度，第 j 列 1 的个数就是顶点 j 的入度。

带权图（网）：

\[G.arcs[i][j]=\begin{cases} w_{ij} &v_i\ne v_j ,\ (v_i, v_j)∈E\\ 0 & v_i=v_j\\ \infin & else \end{cases}\]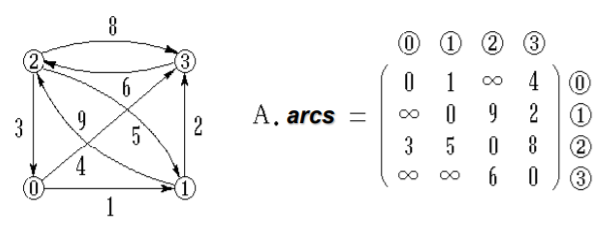

代码实现：

class AdjMatrix{
    int mat[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
};

class MGraph{
    VertexType vexs[MAX_VERTEX_NUM]; //顶点表
    AdjMatrix arcs; //邻接矩阵
    int vexnum,arcnum; //图的顶点数和弧数
};

2、邻接表

邻接表的结构如下：

// 边结点（链式）
class EdgeNode {
 public:
	int adjvex; //这条边指向哪个顶点
	int weight;	//权值
	EdgeNode* next; //指向下一条依附该顶点的边
};
// 顶点结构
class VertexNode {
 public:
	int value; //顶点的值
	EdgeNode *firstedge;	//指向第一条依附该顶点的边
};
// 图结构
class GraphList {
 public:
	VertexNode adjList[N]; //顶点信息
	int numVertex; //顶点数
	int numEdges; //边数
};

下面的图所得到的邻接表如下图所示：

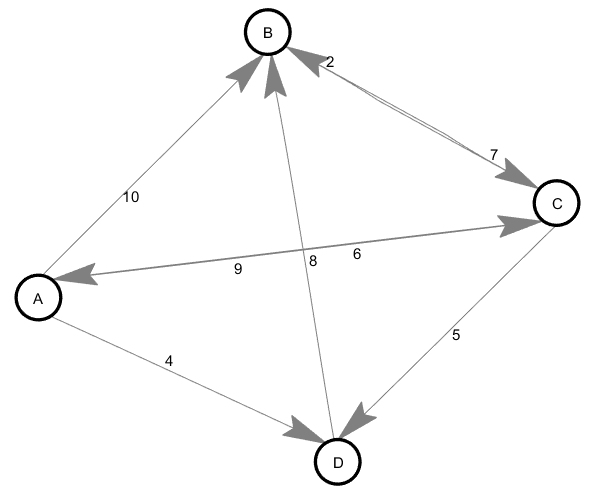
adr value firstedge (adjvex,weight)
0 A -> 1(10) -> 2(6) -> 3(4)
1 B -> 2(7)
2 C -> 1(9) -> 3(5)
3 D -> 1(8)

同时还有存储入边的逆邻接表：

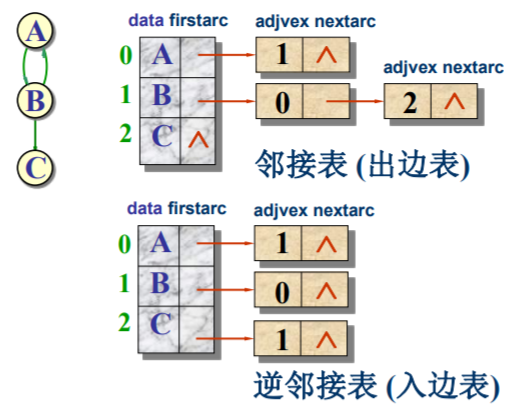
已知存储结构，接下来我们需要根据输入，完成函数void createGraph(GraphList* g)，使用邻接表的方式来实现有向图的创建。输入包含3个部分：

  1. 两个整数v、e，表示图的顶点与边的个数。
  2. v个数，表示各个顶点的值。、
  3. e行输入，每行有三个数：vi、vj、w，分别表示从结点i到结点j的边与其权值。
void createGraph(GraphList* g){
	int v,e;
	cin>>v>>e;
	g->numVertex=v;
	g->numEdges=e;
	//图的顶点与边的个数，构建图
	for(int i=0;i<v;i++){
		cin>>g->adjList[i].value;
	}//各个顶点的值，构建顶点
	for(int i=0;i<e;i++){
		int vi,vj,w;
		cin>>vi>>vj>>w;
		EdgeNode* newe=new EdgeNode;//创建一条新的边
		newe->weight=w;//边的权值
		newe->adjvex=vj;//边指向vj
		EdgeNode *p;
		p=g->adjList[vi].firstedge; //这条边以vi开头
		if(p==NULL){
		  g->adjList[vi].firstedge=newe;
		}
		else {
		  while(p->next != NULL){
		      p=p->next;
		  }
		  p->next=newe;
		}//将这条边连接至边结点的最后
	}//构建边
}

在邻接表中，我们可以通过g->adjList[i]访问每一个顶点；令p=g->adjList[i].firstedge，则p所指向的链表的长度为点i的出度；如果需要得到点i的入度，需要依次访问所有的点，统计所有的p->adjvex：

int count[g->numVertex];//统计入度
for(int i=0;i<g->numVertex;i++){
  	count[i]=0;
}
for(int i=0;i<g->numVertex;i++){
	   EdgeNode *p=g->adjList[i].firstedge;
	   while(p){
		  count[p->adjvex]++;
		  p=p->next;
	   }
}

二、图的遍历

1、深度优先搜索DFS

  1. 从图中的某个顶点v出发，访问之；
  2. 依次从顶点v的未被访问过的邻接点出发，深度优先遍历图，直到图中所有和顶点v有路径相通的顶点都被访问到；
  3. 若此时图中尚有顶点未被访问到，则另选一个未被访问过的顶点作起始点，重复上述（1）（2）的操作，直到图中所有的顶点都被访问到为止。（递归执行，与树的前中后序遍历思路相似）

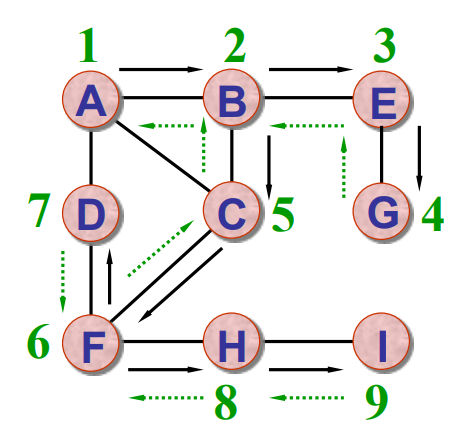
在代码实现时，利用了一个辅助数组visit，用于标记该结点是否已经被访问。

代码实现如下：

/*
图以邻接表形式储存
*/
void DFS(GraphList *g,int i,int *visited){
	cout<<g->adjList[i].value<<" "; //访问该点
	visited[i]=1;//已访问标记
	EdgeNode *p;
	p=g->adjList[i].firstedge;//找到该点的第一个邻接点
	while(p!=NULL){
		if(visited[p->adjvex]==0)
		  DFS(g,p->adjvex,visited);//当该邻接点未被访问时，递归访问该邻接点
		p=p->next;//寻找下一个邻接点
	}
}

void DFSTraverse(GraphList *g){
	int *visited= new int [g->numVertex];
	for(int i=0;i<g->numVertex;i++){
	   visited[i]=0;
	} //visited数组记录点是否已经访问
	for(int i=0;i<g->numVertex;i++){//依次访问图中顶点
	   if(visited[i]==0)DFS(g,i,visited);//当该点没被访问过，进行深度优先搜索
	}
	delete [] visited;
}

2、广度优先搜索BFS

  1. 从图中的某个顶点v出发，访问之；
  2. 依次访问顶点v的各个未被访问过的邻接点，将v的全部邻接点都访问到；
  3. 分别从这些邻接点出发，依次访问它们的未被访问过的邻接点，直到图中所有已被访问过的顶点的邻接点都被访问到。（利用队列结构实现，与层序遍历思路相似）
  4. 入队时访问该顶点，出队时将该顶点所有未被访问的邻接点依次入队。

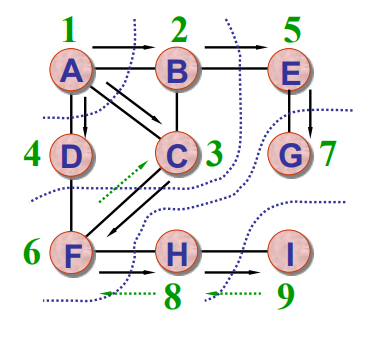
代码实现如下：

/*
图以邻接表形式储存
*/
void BFS(GraphList *g,int i,int *visited){
	cout<<g->adjList[i].value<<" "; //访问该顶点
	visited[i]=1;	//已访问标记
	queue<int> q;	
	q.push(i); //将起始点入队
	while(!q.empty()){
	//每个while循环将一个顶点出队，并依次访问其所有邻接点
		int w=q.front();
		q.pop();
		EdgeNode *p;
		p=g->adjList[w].firstedge;//用于访问所有邻接点
		while(p!=NULL){//访问邻接链表中的所有邻接点
			if(visited[p->adjvex]==0){
				cout<<g->adjList[p->adjvex].value<<" "; //访问该顶点
				visited[p->adjvex]=1;//已访问标记
				q.push(p->adjvex);
			}
			p=p->next;
		}
	}
}

void BFSTraverse(GraphList *g){
	int *visited= new int [g->numVertex];
	for(int i=0;i<g->numVertex;i++){
		visited[i]=0;
	}//visited数组记录点是否已经访问
	for(int i=0;i<g->numVertex;i++){
		if(visited[i]==0)BFS(g,i,visited);//依次对未被访问过的顶点进行广度优先搜索
	}
	delete [] visited;
}

两种遍历方法，使用邻接矩阵表示时，总的时间代价均为$O(n^2)$。

使用邻接表表示时，深度优先搜索扫描边的时间为O(e)，而且对所有顶点递归访问1次，所以遍历图的时间复杂性为O(n+e)；广度优先搜索循环的总时间代价为$d_0 + d_1 + … + d_{n-1} = O(e)$，其中的$d_i$是顶点 i 的度。

三、最小生成树

  • 尽可能用网络中权值最小的边；
  • 必须使用且仅使用 n-1 条边来联结网络中的 n个顶点；
  • 不能使用产生回路的边。

1、Prim算法

选择新的边时必须有一个顶点在已构成的树中。

假设共有n个顶点，我们需要设置一个辅助数组closedge[n]，该数组包含两个元素：

  • lowcost[i]：（当前操作时）生成树内顶点与该顶点相连的最短的边的权值；起始顶点为0，未直接相连的顶点为∞。
  • adjvex[i]：（当前操作时）与该顶点距离最近的生成树内顶点的值，生成树内的顶点的该值为-1。
class closedge{
	int lowcost,adjvex;
};//辅助数组

class TreeNode{
	int vi,vj;
	int weight;
};//生成树

以下图为例，我们一步步得到最小生成树。

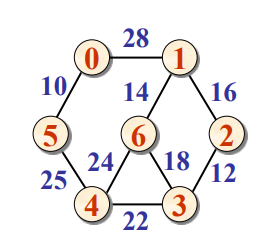
  • 首先将0作为起始点，初始化数组：

  • 我们需要进行n-1次循环，每次循环将一个点加入最小生成树中；

  • 在每一次循环中，寻找adjvex[i]!=-1中lowcost[i]最小所对应的i，对i进行操作：

  • 将该顶点加入生成树中：adjvex[i]=-1，并将边[i,j,w]存入生成树集合；

  • 读取与该顶点相连的边[i,j]，当adjvex[j]!=-1时（不形成环），比较每条边的权值与lowcost[j]的大小，令其取最小值，并令adjvex[j]=i；

  • 完成所有循环后，说明adjvex[i]的值均为-1，lowcost[i]的和为总权值。

N 0 1 2 3 4 5 6
lowcost 0 28 ∞ ∞ ∞ 10 ∞
adjvex -1 0 0 0 0 0 0
N 0 1 2 3 4 5 6
lowcost 0 28 ∞ ∞ 25 10 ∞
adjvex -1 0 0 0 5 -1 0
N 0 1 2 3 4 5 6
lowcost 0 28 ∞ 22 25 10 24
adjvex -1 0 0 4 -1 -1 4
N 0 1 2 3 4 5 6
lowcost 0 28 12 22 25 10 18
adjvex -1 0 3 -1 -1 -1 3
N 0 1 2 3 4 5 6
lowcost 0 16 12 22 25 10 18
adjvex -1 2 -1 -1 -1 -1 3
N 0 1 2 3 4 5 6
lowcost 0 16 12 22 25 10 14
adjvex -1 -1 -1 -1 -1 -1 1
N 0 1 2 3 4 5 6
lowcost 0 16 12 22 25 10 14
adjvex -1 -1 -1 -1 -1 -1 -1

最终得到最小生成树：

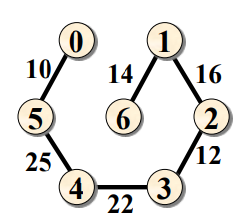
我们以邻接表存储图，代码实现该算法：

class closedge{
	int lowcost,adjvex;
};//辅助数组

class TreeNode{
	int vi,vj;
	int weight;
};//生成树

void Prim(GraphList G, MST& T, int u ) {//u为起点 
	float lowcost[G.NumVertices];
	int nearvex[G.NumVertices];
	for ( int i = 0; i < G.NumVertices; i++ ) {
		lowcost[i] = G.Edge[u][i]; //Vu到各点代价
		adjvex[i] = u; //及最短带权路径
	} 
	adjvex[u] = -1; //加到生成树顶点集合
	int k = 0; //存放最小生成树的结点
	for ( i = 0; i < G.NumEdges-1; i++ )//循环n-1次, 加入n-1条边
  {
		if ( i != u ) 
    { 
				EdgeData min = MaxValue; 
		int v = 0;
		for ( int j = 0; j < NumVertices; j++ )
			if ( adjvex[j] != -1 && lowcost[j] < min )
      { // =-1不参选
				v = j; 
				min = lowcost[j]; 
			}
		//求生成树外顶点到生成树内顶点具有最小权值的边, v是当前具最小权值的边
		if ( v ) 
    { //v=0表示再也找不到要求顶点
			T[k].tail = adjvex[v]; //选边加入生成树
			T[k].head = v;
			T[k].cost = lowcost[v];
			k++; 
			adjvex[v] = -1; //该边加入生成树标记
			for ( j = 0; j < G.n; j++ )
			if ( adjvex[j] != -1 && G.Edge[v][j] < lowcost[j] ) 
      {
				lowcost[j] = G.Edge[v][j]; //修改
				adjvex[j] = v;
			}
		} 
	}
}

2、Kruskal算法

选择新的边时选择最小的不成环的边构成树。

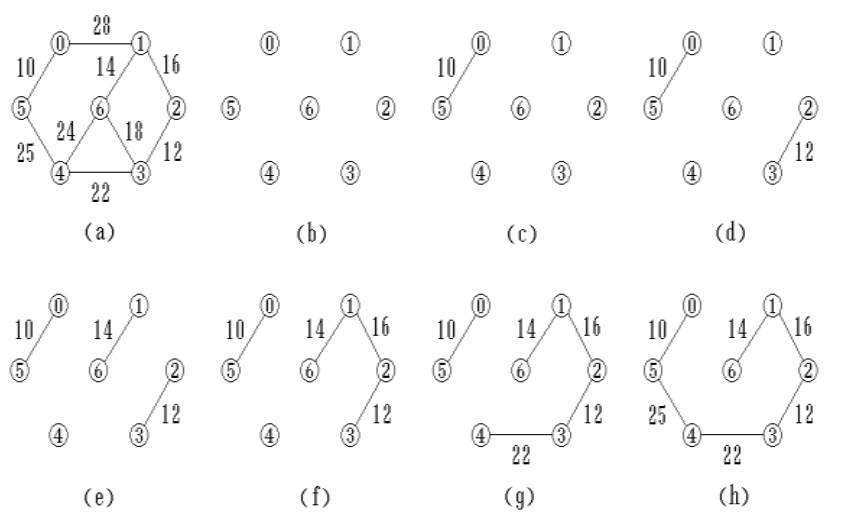
代码实现：

typedef int Vertex;//顶点信息 
struct Edge//边的信息 
{
	Vertex begin;
	Vertex end;
	int edge;//边的权值 
};

int n;//顶点数 
int m;//边的数目
Edge Graph[5000];//以边存储图 
int pre[110];//并查集基本操作 
int sum;//最小的生成树权值和

void Init()
{
	for(int i=1;i<=n;i++)
	{
		pre[i]=i;
	}
}

int find(int x)
{
	int r=x;
	while(pre[r]!=r)
		r=pre[r];
	int i=x,j;
	while(i!=r)
	{
		j=pre[i];
		pre[i]=r;
		i=j;
	}
	return r;
}

void join(int x,int y)
{
	int fx=find(x);
	int fy=find(y);
	if(fx!=fy)
		pre[fx]=fy;
}
bool comp(Edge a,Edge b)//对边权值进行排序 
{
	return a.edge<b.edge;
}
void Kruskal() 
{
	sort(Graph,Graph+m,comp);//排序，最小权值的边最先 
	int number=0; //记录当前用于连接顶点的边数 
	Init();//初始化并查集 
	sum=0;
	for(int i=0;i<m;i++)
	{
		if(number==n-1)//n个顶点若连接n-1条边，则图已经连通 
			break;
		if(find(Graph[i].begin)!=find(Graph[i].end))//当前边所连接的顶点处于未连通的状态 
		{
			join(Graph[i].begin,Graph[i].end);
			sum+=Graph[i].edge;
			number++;
		}
	}
}

四、AOV网（拓扑排序）

1、算法思路

  1. 输入AOV网。令n为顶点个数。
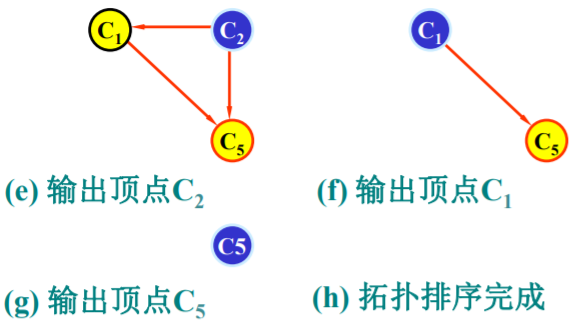
  2. 在AOV网络选一个入度为0的顶点,并输出之;
  3. 从图中删去该顶点, 同时删去所有以它为出度的有向边，更新剩余点的入度;（只需要判断发生更新的顶点的入度是否为零，不需要再次遍历一次数组count）
  4. 重复以上2、3步, 直到全部顶点均已输出，拓扑序列形成，拓扑排序完成；或图中还有未输出的顶点, 但已跳出处理循环：说明图中还剩下的顶点入度都不为0，这时网络中必存在有向环。
  5. 为了得到所有顶点的入度，我们在邻接表中增设一个数组count[ ]，记录各顶点入度。
  6. 使用一个存放入度为0的顶点的链式栈/队列, 供选择和输出入度为0的顶点。

20

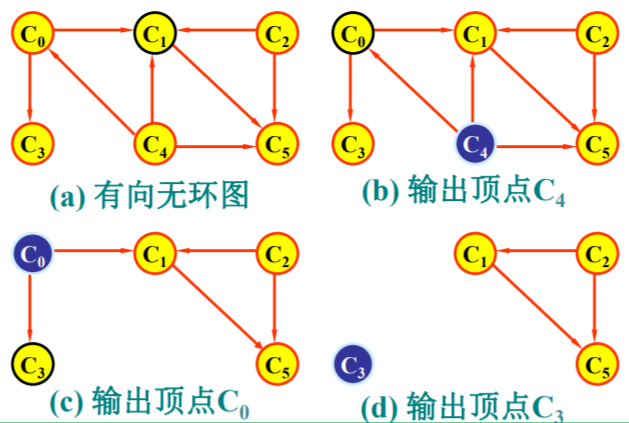
2、代码实现

void Graphcircle(GraphList *g){
	int count[g->numVertex],del[g->numVertex];
		for(int i=0;i<g->numVertex;i++){
			count[i]=0;
		}
	for(int i=0;i<g->numVertex;i++){
		EdgeNode *p=g->adjList[i].firstedge;
		while(p){
			count[p->adjvex]++;
			p=p->next;
		}
	}//初始化count,得到所有顶点的入度
	stack<int> sta;
	int num=0;
	for(int i=0;i<g->numVertex;i++){
		if(count[i]==0){
			sta.push(i);
		}
	}//将初始时所有入度为0的顶点入栈 
	while(!sta.empty()){
		int w=sta.top();
		sta.pop();//弹出一个顶点，对其进行操作
		//cout<<g->adjList[w].value; //输出排序
		num++;//统计弹出顶点数
		EdgeNode *p=g->adjList[w].firstedge;//访问该顶点的邻接点
		while(p){
			count[p->adjvex]--;
      if(count[p->adjvex]==0){
         sta.push(p->adjvex);
      }//更新剩余顶点的入度，并马上判断是否有新的顶点入度为0
			p=p->next;
		}
	} 
	 if(num==g->numVertex) cout<<"no circle";//无环，得到拓扑排序
	 else cout<<"has circle";//有环
}

五、AOE网

1、定义

无有向环的带权有向图中：

  • 用有向边表示一个工程中的各项活动(Activity)
  • 用边上的权值表示活动的持续时间(Duration)
  • 用顶点表示事件(Event)

2、求完成工程所需最短时间

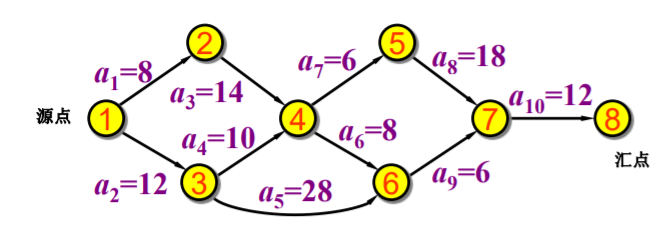
入度为零的点叫源点，出度为零的点叫汇点。完成整个工程所需的时间取决于从源点到汇点的最长路径长度，这条路径长度最长的路径就叫做关键路径，路径上的活动叫做关键活动。

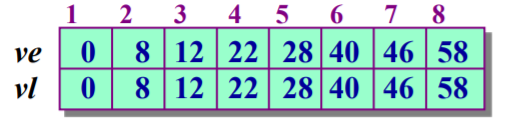
使用邻接矩阵mat[][]存储图，利用4个辅助数组ve[]，vl[]，e[]，l[]进行计算，以下的顶点$v_0$指所有入度为零的点，顶点$v_{n-1}$指所有入度为零的点：

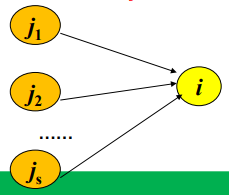
ve[i]：事件最早发生时间，源点$v_0$到顶点$v_i$的最长路径长度。

可从ve[0]开始递推，ve[0]=0，ve[j]=max(ve[j]，ve[i]+mat[i][j])，此时必须确保点j的最早发生时间已确定，具体实现时需要使用拓扑排序。

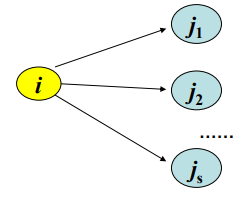
vl[i]：事件最迟允许时间，是在保证汇点$v_{n-1}$在ve[n-1] 时刻完成的前提下，事件$v_{i}$的允许的最迟开始时间。

可从vl[n-1]开始递推，vl[n-1]=ve[n-1]，vl[i]=min(vl[i]，vl[j]-mat[i][j])，此时必须确保点j的最迟允许时间已确定，具体实现时需要逆序使用拓扑排序。

设活动k在路径<i,j>上：

e[i]：活动最早发生时间，直接通过e[k] = ve[i]得到即可。

l[i]：活动最迟允许时间，直接通过l[k] = vl[j] - mat[i][j]得到。

当l[k] == e[k]时，活动k就是关键活动，所有关键活动组成关键路径。

22

24

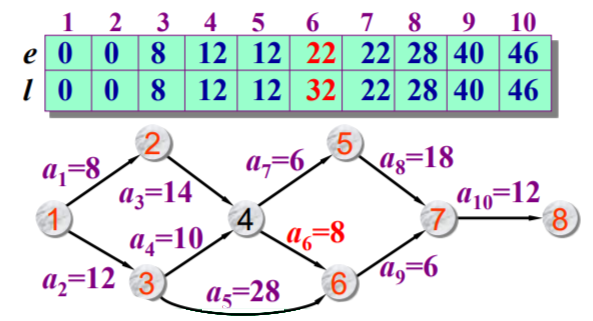
3、代码实现

void AOE(){
	int n,m;
	cin>>n>>m;
	int mat[n][n],ve[n],vl[n],e[m],l[m],edge[m][2];
	for(int i=0;i<n;i++){
		ve[i]=-1;
		vl[i]=999;
		for(int j=0;j<n;j++)
			mat[i][j]=0;
	}
	for(int i=0;i<m;i++){
		int a,b,w;
		cin>>a>>b>>w;
		mat[a][b]=w;
		edge[i][0]=a;
		edge[i][1]=b;
	}
	
	//拓扑 
	int count[n];
	for(int i=0;i<n;i++){
        count[i]=0;
	}
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			if(mat[i][j]>0)count[j]++;
		}
	}
	stack<int> sta,last;
	int num=0;
	for(int i=0;i<n;i++){
		if(count[i]==0){
			sta.push(i);
			ve[i]=0;
		}
	}//第一个入栈 
	while(!sta.empty()){
		int w=sta.top();
		sta.pop();
    last.push(w);
		for(int i=0;i<n;i++){
			if(i!=w && mat[w][i]!=0){
				count[i]--;
				ve[i]=max(ve[i],ve[w]+mat[w][i]);
				if(count[i]==0)
					sta.push(i);
       }    
		}
	}
	int w=last.top();
	vl[w]=ve[w];
	while(!last.empty()){
		int w=last.top();
		last.pop();
		for(int i=0;i<n;i++){
			if(i!=w && mat[i][w]!=0){
				vl[i]=min(vl[i],vl[w]-mat[i][w]);
			}			   
		}
	}
	
	for(int i=0;i<m;i++){
		e[i]=ve[edge[i][0]];
		l[i]=vl[edge[i][1]]-mat[edge[i][0]][edge[i][1]];
	} 
	
	for(int i=0;i<n;i++){
		cout<<ve[i]<<"\t";
	}
	cout<<endl;
	for(int i=0;i<n;i++){
		cout<<vl[i]<<"\t";
	}cout<<endl;
	
	for(int i=0;i<m;i++){
		cout<<e[i]<<"\t";
	}
	cout<<endl;
	for(int i=0;i<m;i++){
		cout<<l[i]<<"\t";
	}
	cout<<endl;
	return 0;
}

六、最短路径

1、从一个起点到任意顶点的最短路径：Dijkstra算法

为了实现算法，我们引用3个辅助数组：

  • dist[i]：用于记录到点i的最短路径长度。
  • path[i]：用于记录到点i的最短路径的前一个顶点。
  • S[i]：记录点i是否已知最短路径。

算法步骤如下——

  1. 初始化辅助数组；
  2. 找到未知最短路径中路径最短的顶点，加入已知顶点中（操作S）；
  3. 修改以该顶点为起点的顶点的最短路径与上一个顶点（操作dist和path）；
  4. 重复n-1次，直到所有顶点都已知。

以下面的图为例：

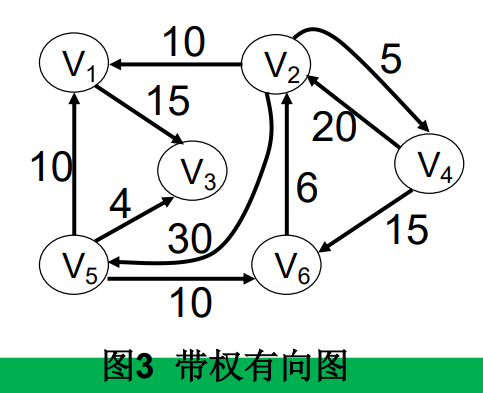
初始化：

i v1 v2 v3 v4 v5 v6
dist[i] ∞ 20 ∞ 0 ∞ 15
path[i] -1 4 -1 4 -1 4
S[i] 0 0 0 1 0 0

V6：

i v1 v2 v3 v4 v5 v6
dist[i] ∞ 20 ∞ 0 ∞ 15
path[i] -1 4 -1 4 -1 4
S[i] 0 0 0 1 0 1

V2：

i v1 v2 v3 v4 v5 v6
dist[i] 30 20 ∞ 0 50 15
path[i] 2 4 -1 4 2 4
S[i] 0 1 0 1 0 1

V1：

i v1 v2 v3 v4 v5 v6
dist[i] 30 20 45 0 50 15
path[i] 2 4 1 4 2 4
S[i] 1 1 0 1 0 1

V3：

i v1 v2 v3 v4 v5 v6
dist[i] 30 20 45 0 50 15
path[i] 2 4 1 4 2 4
S[i] 1 1 1 1 0 1

V5：

i v1 v2 v3 v4 v5 v6
dist[i] 30 20 45 0 50 15
path[i] 2 4 1 4 2 4
S[i] 1 1 1 1 1 1

代码实现如下：

void Dijkstra(){
	int n,m,v;//顶点数n、边数m、起点v 
	cin>>n>>m>>v;
	int mat[n][n];//邻接矩阵 
	int dist[n],path[n],S[n];//三个辅助数组 
	for(int i=0;i<n;i++){
		dist[i]=0;
		path[i]=-1;
		S[i]=0;
		for(int j=0;j<n;j++)
			mat[i][j]=0;
	}//数组初始化 
	for(int i=0;i<m;i++){
		int a,b,w;
		cin>>a>>b>>w;
		mat[a][b]=w;
	}//邻接矩阵输入 
	dist[v]=0;
	path[v]=v;
	S[v]=1;
	for(int i=0;i<n;i++){
		if(mat[v][i]>0){
				dist[i]=mat[v][i];
				path[i]=v;
		}
	}//算法初始化 
//	for(int j=0;j<n;j++){
//		cout<<dist[j]<<"\t";
//	}
//	cout<<endl;
//	for(int j=0;j<n;j++){
//		cout<<path[j]<<"\t";
//	}
//	cout<<endl;
//输出检测
	for(int i=0;i<n-1;i++){//执行n-1个循环，依次确定每个点的最短路径 
		int min=999,min_ind=0;
		for(int j=0;j<n;j++){
			if(S[j]==0){
				if(min>dist[j]){
					min=dist[j];
					min_ind=j;
				}
			}
		}//找到未得到最小路径的点中的最小值
		S[min_ind]=1;//该点确定最小路径，添加至S
		for(int j=0;j<n;j++){
			if(mat[min_ind][j]>0){
				if(dist[j]>(dist[min_ind]+mat[min_ind][j])){
					dist[j]=dist[min_ind]+mat[min_ind][j];//修改路径长度 
					path[j]=min_ind;//标记路径 
				}
			}
		}
	}
    return 0;
}

2、任意顶点间最短路径：Floyd算法

算法思路与Dijkstra算法相同，不过直接对邻接矩阵进行操作，得出所有顶点间的路径，时间复杂度为$O(n^3)$。

邻接矩阵A[i][j]存储最小路径<i,j>；增加一矩阵path[i][j]存储当前路径下顶点j的上一顶点。

矩阵$A_{k+1}$得到的路径是路线中间点序号不超过k的最短路径，最终得到不超过n-1的最短路径，即最终路径。

邻接矩阵递推关系如下：


\(A_{k+1}[i][j]=min(A_k[i][j],A_k[i][k]+A_k[k][j])\\ P[i][j]==\begin{cases} P[i][j]\ \ A[i][j]更小\\ P[k][j]\ \ A[i][k]+A[k][j]更小 \end{cases}\)
算法步骤如下——

  1. 初始化邻接矩阵与路线矩阵；
  2. 根据递推式修改邻接矩阵A与路线矩阵path；
  3. 重复n次，得到所有最短路径。

示例：

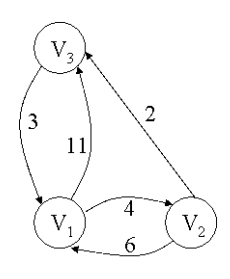
代码实现如下：

void Floyd(){
	int n,m;//顶点数n、边数m
	cin>>n>>m;
	int mat[n][n];//邻接矩阵 
	int path[n][n];//三个辅助数组 
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			mat[i][j]=999;
			path[i][j]=-1;
		}
		mat[i][i]=0;
		path[i][i]=i;
	}//数组初始化 
	for(int i=0;i<m;i++){
		int a,b,w;
		cin>>a>>b>>w;
		mat[a][b]=w;
		path[a][b]=a;
	}//算法初始化 
	for(int k=0;k<n;k++){
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				//当新的路径更加短时，更新mat和path
				if(mat[i][j]>mat[i][k]+mat[k][j]){
					mat[i][j]=mat[i][k]+mat[k][j];
					path[i][j]=path[k][j];
				}
			}
    }
	}
//	for(int i=0;i<n;i++){
//		for(int j=0;j<n;j++){
//			cout<<mat[i][j]<<"\t";
//		}
//		cout<<endl;
//	}
//	cout<<endl;
//输出检测
	return 0;
}

图小结

CATALOG
    FEATURED TAGS
    C++ test 俄罗斯方块 MFC Github jekyll 搭建博客 魔方 盲拧 Ubuntu 数据结构 CPU 计算机组成原理 openCV 相机标定 实验室 NEON 线性结构 算法 操作系统 Matlab 双目匹配 Python 图像压缩 OpenCV 图像处理 SIMD 并行与分布式 数值计算 C Linux 信号与系统 分布式
    FRIENDS