文件管理
数据以文件的方式存储在外存,需要进行有效的管理。
一、基本概念
1、基本概念
数据项(item、field):数据文件中最小单位,反映实体某一方面的属性的数据表示。
记录(record):一个实体的所有数据项的集合,用来表示一个记录的数据项集合称为关键字项。
文件(file):大量性质相同的数据记录的集合。
逻辑结构:记录间在逻辑上的线性结构。
基本物理结构(在存储空间:外存上的组织方式):顺序结构、链接结构、索引结构
2、文件分类
(1)按记录类型:
- 操作系统文件:连续的字符串集合;
- 数据库文件:有特定结构(一个数据库内的所有记录结构相同)堆数据记录集合。
(2)按记录长度:
- 定长记录文件:每个记录都有固定的数据项,数据项长度固定。
- 不定长记录文件
3、文件操作
(1)检索记录:从文件中查找相应记录;
(2)插入记录:把给定的记录插入文件的指定位置。(先检索插入点位置,再插入)
(3)删除记录:删除给定记录。(条件/位置)
(4)修改记录:检索符合修改条件的记录,进行修改。
(5)记录排序:根据指定关键字,对文件中的记录按照关键字大小重新排列/存储。
二、文件组织方式
1、顺序文件
记录的逻辑顺序和存储顺序是一致的,可分为连续/链接顺序文件,排序/一般顺序文件。
类似线性表的顺序存储结构。
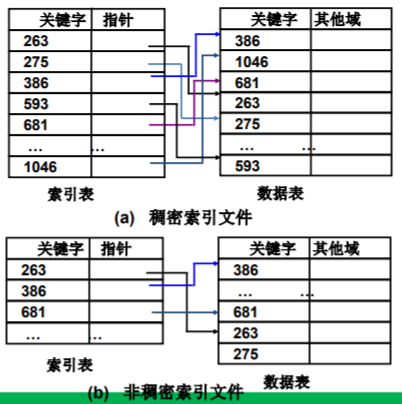
2、索引文件
由索引表、数据表构成。
数据表:存储实际数据记录。
索引表:存储记录的关键字和记录地址之间对照关系(关键字->地址->数据表)
3、ISAM文件
顺序索引存取方法,采用静态索引结构,专门为磁盘设计。
有三个索引目录,磁道索引、柱面索引和主索引,类似于柱坐标系。
在每一个柱面上还有一个溢出区,存放溢出的记录。索引项有基本索引项和溢出索引项。
4、VSAM文件
虚拟存取方法,利用虚拟存储器功能,基于B+树的动态索引结构。
由索引集、顺序集和数据集构成。
5、散列文件
又称直接存取文件,类似散列表(哈希表),将记录散列存储到存储介质上。
记录成组存放,若干个记录形成一个存储单位:桶。同一个桶中的记录关键字相同。若存储了n个记录的桶要加入第n+1个记录,则发生了溢出。
6、多关键字文件
数据库文件,可以对主关键字、次关键字都进行查询,需要对各个关键字都进行索引。
可以用多重表文件或倒排文件实现。
算法分析
- 问题分析:准确、完整地理解和描述问题
- 数学模型建立
- 算法设计与选择:创造性的活动
- 算法表示:思想的表示形式
- 算法分析:算法时空特性分析
- 算法实现
- 程序调试:测试
- 结果整理文档编制
一、算法基本技巧
1、算术运算
例: 开灯问题
有从1到n依次编号的n个同学和n盏灯。1号同学将所有的灯都关掉;2号同学将编号为2的倍数的灯都打开;3号同学则将编号为3的倍数的灯作相反处理(该号灯如打开的,则关掉;如关闭的,则打开);以后的同学都将自己编号的倍数的灯,作相反处理。
问:经 n个同学操作后,哪些灯是打开的?
算法思路:
用数组a[n]表示灯,用1、0表示灯灯开与关;
可以用a[i] = 1 - a[i]代替if(a[i] == 1)a[i] = 0的判断操作。
2、标志量
flag = 1
3、信息数字化
例: 警察抓小偷
警察局抓了a,b,c,d四名偷窃嫌疑犯,其中只有一人是小偷。审问中:
- a说:“我不是小偷。”
- b说:“c是小偷。”
- c说:“小偷肯定是d。”
- d说:“c在冤枉人。”
现在已经知道四个人中三人说的是真话,一人说的是假话,问到底谁是小偷?
设小偷为x,四个人的话可以转化为表达式:x != 1、x == 3、x == 4、x != 4
结果表达式为:(x != 1) + (x == 3) + (x == 4) + (x !=4) == 3
二、算法设计方法
1、分治/递归
对于一个规模为n的问题P(n),可以把它分解为k个规模较小的子问题,这些子问题互相独立,且结构与原来问题的结构相同。在解这些子问题时,又对每一个子问题进行进一步的分解,直到某个阈值n0为止。递归地解这些子问题,再把各个子问题的解合并起来,就得到原问题的解。
适用条件:
- 该问题的规模缩小到一定的程度就可以容易地解决;
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
- 利用该问题分解出的子问题的解可以合并为该问题的解;
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共 的子问题。
步骤:
- 1)分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
- 2)解决:若子问题规模较小而容易被解决则直接解,否则再继续分解为更小的子问题,直到容易解决;
- 3)合并:将已求解的各个子问题的解,逐步合并为原问题的解。
例:二进制大整数乘法
两个n位大整数x、y相乘:
$x = a+b = a2^{n/2}+b,(a.size=b.size=n/2)$ $y = c+d = c2^{n/2}+d,(c.size=d.size=n/2)$ $xy = ac2^n+(ad+bc)2^{n/2}+bd$
上述式子用了ac、ad、bc、bd四次乘法,可以优化为:
$xy = ac2^n+((a-b)(d-c)+ac+bd)2^{n/2}+bd$
只进行了ac、bd、(a-b)(d-c)三次乘法。
例:多项式乘积
计算两个n阶多项式的乘法:
$p(x) = a_0x^0+a_1x^1+a_2x^2+\dots+a_nx^n$ $q(x) = b_0x^0+b_1x^1+b_2x^2+\dots+b_nx^n$
采用一般的方法计算,需要(n+1)2次乘法运算和n(n+1)次加法运算。
优化:
将一个多项式分为两个:
$p(x) = p_0(x) + p_1(x)x^{n/2}$
$q(x) = q_0(x) + q_1(x)x^{n/2}$
则:
$p(x)q(x) = p_0(x)q_0(x)+[p_0(x)q_1(x)+p_1(x)q_0(x)]x^{n/2}+p_1(x)q_1(x)x^n$
引入:
$r_0(x) = p_0(x)q_0(x)$
$r_1(x) = p_1(x)q_1(x)$
$r_2(x) = [p_0(x)+p_1(x)][q_0(x)+q_1(x)]$
则可以转化为:
$p(x)q(x) = r_0(x)+[r_2(x)-r_1(x)-r_0(x)]x^{n/2}+r_1(x)x^n$
减少了一次乘法运算。
例:棋盘覆盖
在一个$2^k\times 2^k$个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
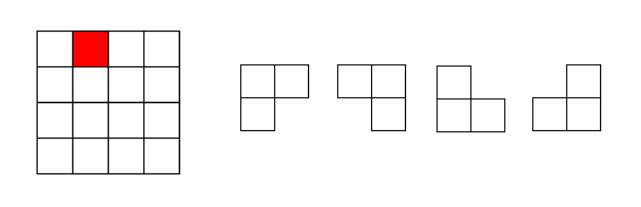
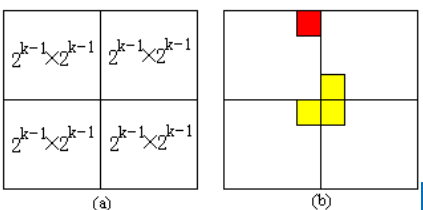
划分:
将$2^k\times 2^k$棋盘分割为4个$2^{k-1}\times 2^{k-1}$子棋盘(a)所示。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如 (b)所示,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为2×2棋盘。
![](/assets/post_img/2019-12-24/3.png