零、图像存储
我们知道,计算机是通过像素存储一张图片的,每张图片都由AxB个像素点构成,只要存储每个像素点包含的信息,就能存储一张图片。
如果图片是黑白的,那每个像素点需要8bit的空间存储,表示其灰度值(0-255);如果图片是彩色的,一般来说会使用RGB存储,一共需要24bit=3B的空间存储。
那一张1024x1024大小的图片(与一般的图片大小接近,取1024便于计算),则一共需要$2^{20} \times 3B = 3MB$的空间,如果计算机真的以这种形式存储图片,那么空间消耗是巨大的,所以需要利用更加精巧的方式存储这些数据。
这些存储方式的体现,就是我们平时使用的jpg、png、gif等图片格式了,每种图片格式都对应着一种对“记录像素RGB的原始数据”的处理方式(可以理解为编码),计算机会根据图片格式去解读这张图片的二进制数据,然后将这张图片展示出来(可以理解为解码)。
这种处理数据的方式就称为压缩,而压缩可以分为两种:
- 无损压缩:处理数据之后没有丢失任何数据,比如将(2,2,2,2,2,2,2,2,2,2)十个数表示为(2,10),以表示10个连续的2。这两者所包含的信息并没有区别,而空间存储上实现了压缩。
- 有损压缩:在处理数据的过程中去除了“不必要”的信息,对图像而言,可以理解为去除了冗余的图像和彩色数据,所以压缩得到的图像和源图像有所区别,且无法复原成原来图片的样子。
下面我们看一看JPEG图片格式:
JPEG是Joint Photographic Experts Group(联合图像专家组)的缩写,文件后辍名为”.jpg”或”.jpeg”,是最常用的图像文件格式,由一个软件开发联合会组织制定,是一种有损压缩格式,能够将图像压缩在很小的储存空间,图像中重复或不重要的资料会被丢失,因此容易造成图像数据的损伤。尤其是使用过高的压缩比例,将使最终解压缩后恢复的图像质量明显降低,如果追求高品质图像,不宜采用过高压缩比例。
简单来说,JPEG图片格式就是一种有损压缩格式,可以用较少的磁盘空间得到较好的图像质量。
那么,它是如何实现对图像进行压缩的呢?其压缩流程一般如下:
图像分割——颜色空间转换——DCT——数据量化——编码
接下来开始一步一步说明压缩方式。
一、图像分割
为了处理的方便,JPEG将图片分割成了多个8x8的区域,对每个区域单独进行处理。
二、颜色空间转换
颜色空间是在某些标准下用通常可接受的方式对彩色加以说明,或者说是人为规定的用数据表示颜色的一种方式。
我们熟知的RGB就是一种颜色空间,利用R、G、B三原色的叠加形成颜色。如果利用RGB空间表示一张8x8的图片,可以视为用3个8x8的矩阵存储颜色信息,解读这三个矩阵即可得到图片。
为了降低数据量,通常把 RGB空间表示的彩色图像转换到其他色彩空间,计算机常用的颜色空间为YCrCb,它使用Y、Cr和Cb三个分量来表示,Y为颜色的亮度、而Cb和Cr则为蓝色和红色的浓度偏移量成份。
由于JPEG格式使用的颜色空间为YCrCb,所以需要将RGB转化为YCrCb。具体转换方式这里也不多赘述,简单理解成利用另一类3个8x8的矩阵存储颜色信息。
不过,JPEG格式的压缩处理方式实际上只是针对数据进行处理,对颜色空间本身无关。RGB、YcbCr颜色空间的不同,只表现为存储颜色信息的矩阵里面的数据不同,对矩阵的处理方式实际上是一样的。
通过上面的处理,在一张图片中我们得到了n个8x8的矩阵,接下来就开始对矩阵数据进行处理,也是本篇博文的核心内容——图像压缩原理。
三、图像压缩原理
这一部分实际上是我写这篇博客的目的,想记录下对数据进行压缩的方式和处理思想。上面有写到,JPEG处理数据的方式是DCT(离散余弦变换),但在介绍DCT之前,我准备先说明一下图像压缩的原理。
为了更简单地理解压缩思想,我们先给出一张图片:

可以看到,图中存在大量高度相似的色彩数据,比如一整片的天空,那一区域的颜色数据一定高度相似。
如果这幅图片是黑白的,那我们只需要一个AxB的矩阵就可以存储它的灰度信息,将其分成多个8x8的矩阵。
我们可以发现,里面大部分矩阵,里面的元素都是相似的,比如截取天空的一个8x8的矩阵,得到数据如下:
\(\begin{bmatrix} 100 & 101 & ... & 99\\ 100 & 98& ... &99 \\ ... & ... & ...& ... \\ 100 & 101 & ... & 100\\ \end{bmatrix}\) 矩阵中的元素都很相似,那么,我们不免想到,可不可以用更加简单的方式表示这些数据,甚至舍去这些数据中少量的细节。
舍去细节,很自然的方式就是将某些数据直接舍去,置为0,但这在上面的矩阵上行不通。如果将这里的某个元素置为0,那其对应的像素点就会变成黑色,换句话说,这个像素点的所有信息都被舍去了。
那么,如果我们换一种方式表示数据,使其中一部分数据携带更多的信息,而使另一部分数据只携带少量信息。然后将另一部分的数据直接舍去,剩余的数据还原成图像,和原图像观感可能并没有什么区别。这就是图像压缩的基本思想:
- 将图像数据用另一种方式表达,使一部分数据只携带少量信息;
- 将这一部分数据舍去,只保留另外大部分的颜色信息。
比如上面的矩阵,如果我们直接使用一个数字:100存储,表示原矩阵的每个元素都是100。如此处理,虽然丢失了部分细节,但直接将数据量压缩至1/64,且由于100携带的信息较多,它与原矩阵的区别并不大。
那么,对于一个矩阵,要如何分离数据,找到值得被舍去的数据。这就和线性代数的线性组合和基有关:
基变换
依旧以上面8x8的矩阵为例,首先,我们将它变成一个64维的向量,即把这个矩阵拉成一列,形成一个64x1的列向量:$x = [100,101,99…..100]^T$
那么,这个向量表示什么?它的每一个元素对应一个像素点的灰度值,那这个向量表示一种线性组合,表示如下:
\[\begin{bmatrix} 100\\ 101\\ ...\\ 100 \end{bmatrix} = 100 \begin{bmatrix} 1\\ 0\\ ...\\ 0 \end{bmatrix} + 101 \begin{bmatrix} 0\\ 1\\ ...\\ 0 \end{bmatrix} +...+ 100 \begin{bmatrix} 0\\ 0\\ ...\\ 1 \end{bmatrix}\] \[\begin{bmatrix} c_0\\ c_1\\ ...\\ c_{63} \end{bmatrix} = c_0 \begin{bmatrix} 1\\ 0\\ ...\\ 0 \end{bmatrix} + c_1 \begin{bmatrix} 0\\ 1\\ ...\\ 0 \end{bmatrix} +...+ c_{63} \begin{bmatrix} 0\\ 0\\ ...\\ 1 \end{bmatrix}\]用线性代数的语言来说,x表示的是64维标准基的一种线性组合,x的元素为各个标准基的系数,其中的每一个基向量包含的信息为一个像素点的灰度值。
n维向量空间($R^n$)可以由n个线性无关的向量的基来表示,但一个向量空间的基并不是唯一的。这就为我们的压缩带来了可能性,如果我们能找到一组基,让其中的几个基包含更多的信息,将另外的基的系数直接置为0,这就能在保留大部分信息的情况下压缩数据大小了。
我们使用4维的向量,以便接下来的讨论,假设一个向量如下:
\[\begin{bmatrix} 40\\ 40\\ 30\\ 30 \end{bmatrix} = 40 \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} + 40 \begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix} + 30 \begin{bmatrix} 0\\ 0\\ 1\\ 0 \end{bmatrix} + 30 \begin{bmatrix} 0\\ 0\\ 0\\ 1 \end{bmatrix}\]我们将它的基换成一类特殊的基:
\(\begin{bmatrix} 40\\ 40\\ 30\\ 30 \end{bmatrix} =c_0 \begin{bmatrix} 1\\ 1\\ 1\\ 1 \end{bmatrix} +c_1 \begin{bmatrix} 1\\ 1\\ -1\\ -1 \end{bmatrix} +c_2 \begin{bmatrix} 1\\ -1\\ 0\\ 0 \end{bmatrix} +c_3 \begin{bmatrix} 0\\ 0\\ 1\\ -1 \end{bmatrix}\) 将其换成矩阵表示: \(b= \begin{bmatrix} 40\\ 40\\ 30\\ 30 \end{bmatrix} = \begin{bmatrix} 1&1&1&0\\ 1&1&-1&0\\ 1&-1&0&1\\ 1&-1&0&-1 \end{bmatrix} \begin{bmatrix} c_0\\ c_1\\ c_2\\ c_3 \end{bmatrix} =Ax\)
矩阵A是我们定义出来的,我们要求的就是$c_0c_1c_2c_3$这几个系数,即x,那可以使用$A^{-1}b = x$求出x。
我们知道,矩阵求逆的运算量是比较大的,不过矩阵A比较特殊:它的每个基相互正交(垂直),A是一个正交矩阵,这就简化了我们的求逆运算:
将每个基单位化(即第一、二个基向量除以4,第三、四个基除以$\sqrt{2}$),这就得到了标准正交矩阵Q,而$Q^{-1} = Q^{T}$,我们只需要将矩阵进行转置,就可以得到矩阵的逆,简化了大量的运算。
上面1与-1相互交替出现的基,称为小波基(Wavelet),可以看出,它的基向量包含的信息是不同的,越靠前的向量包含的信息越多。简单来说,小波基包含的信息是从整体到局部的,越靠后的基向量包含的信息越少,可以被我们所丢弃。
在4维小波基上的体现如下:
\[\begin{bmatrix} c_0\\ c_1\\ c_2\\ c_3 \end{bmatrix} => \begin{bmatrix} c_0\\ c_1\\ 0\\ 0 \end{bmatrix}\]知道了基变换的概念,就可以回到我们64x1的列向量上:$x = [100,101,99…..100]^T$
如果我们将64维的标准基表示转换成64维小波基,再舍去$c_{32}-c_{63}$、甚至$c_{16}-c_{63}$的系数,对图片基本不会造成什么影响,这样就可以对数据进行压缩了。
JPEG格式使用的DCT(离散余弦变换)本质上也是找到另一组基向量,当然所找的基更为复杂,处理时丢失的数据也更少。
四、DCT(离散余弦变换)
离散余弦变换是与傅里叶变换相关的一种变换,它类似于离散傅里叶变换(DFT for Discrete Fourier Transform),但是只使用实数。
当我们要处理的不再是函数,而是一堆离散的数据时,并且这些数据是对称的话,那么傅里叶变化出来的函数只含有余弦项,这种变换称为离散余弦变换。
以向量空间的基来理解的话,它将标准基下的向量$[x_1,x_2…x_n]$由基变换变换成$[F_1,F_2…F_n]$
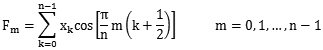
标准基下的每个元素$x_m$都可以表示为:
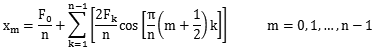
整理成矩阵形式,可以看到一组向量基:
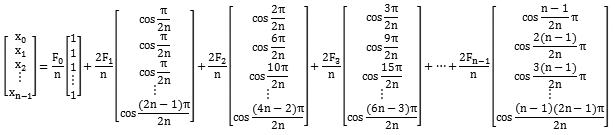
所以这个处理本质上也是一个基变换。
不过,实际上的处理用的是二维离散余弦变换,从一个8x8的矩阵形成一个新的8x8矩阵,将信息密度由高到低从左上角到右下角分布。

在实际压缩处理过程中,图像本身就具有连续性,所以矩阵中的大部分数值都不会出现太大的波动,$F_0$会呈现出一个较大的数值(称为直流分量),其他数值一般偏小(称为交流分量)。只需要将其中不重要的交流分量“舍去”,即可完成我们的压缩操作。
五、数据量化
我们一直提到要舍去“包含信息少”的数据,那么,如何定义这个“少”,又如何进行“舍去”这个操作。数据量化这一步就是用以完成这一操作的。
数据量化简单来说,就是做除法,将DCT操作得到的矩阵A中的元素再进行一次除法操作,得到量化矩阵B。($A => B$)
首先,我们需要一个量化系数矩阵Q,称为量化表。JPEG算法提供了两张标准的量化系数矩阵,分别用于处理亮度数据Y和色差数据Cr以及Cb。
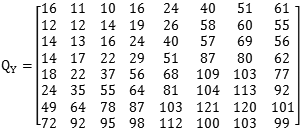
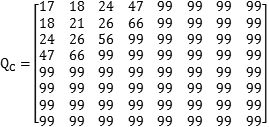
对矩阵A的元素,进行如下计算:$B_{ij} =round(\frac{A_{ij}}{Q_{ij}})$
round为取整函数,进行量化处理后,数据会呈现出如下结果:

可以看到,大部分的数据都变成了0,而且非零的数值也相应变小,可以用更少的数据长度去存储。这一操作的效果就是舍去“包含信息少”的数据,同时,由于量化表的系数,交流分量如果较大,在计算后也不会变成0,可以得到有效保留。
译码数据时,只需要将各元素重新乘以量化表中的元素就可还原。(当然无法完全还原成A,这就是压缩时造成的信息损失)
最后,由于现在还是一个二维矩阵,而计算机的存储空间是一维的,所以我们需要按照如下顺序将其转换成一个一维数组:
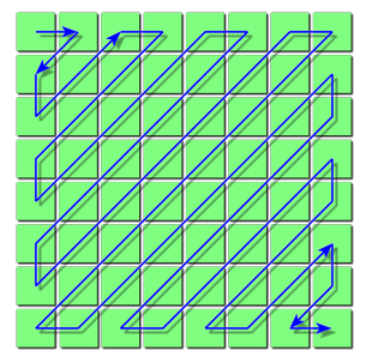
通过这种弯弯曲曲的组织形式,数据中的0都会集中在数组最后,接下来就可以进行最后一步——编码了。
六、编码
编码方式比较简单,下面说说两种常用的编码方式。
1、行程编码
行程编码也叫作RLE压缩编码,其中RLE是Run-Length-Encoding的缩写, 这种压缩方法是最简单的图像压缩方法。
行程编码的基本原理是在给定的数据图像中寻找连续的重复数值,然后用两个字符取代这些连续值。例如,一串字母表示的数据为“aaabbbbccccdddeeddaa”,经过 游程编码处理可表示为“3a4b4c3d2e2d2a”。
2、哈夫曼编码
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
哈夫曼编码方式这里也不多赘述。
经过编码操作之后,图像压缩彻底完成。
七、参考资料
这篇博文学习参考了以下博文,感谢作者们~