一、求幂算法
给定整数x、y,求$x^y$称为求幂运算,最朴素的求法为:
long ans = 1;
for(int i = 0; i<y ;i++)
ans *= x;
这一求法十分直观,但一共需要进行y次乘法,运算复杂度为O(y);我们将y用二进制表示,看看能否减少乘法运算的次数。
二、快速幂
如果想求$x^y$,若y为偶数,则$x^y = (x^{y/2})^2$;如果y是奇数,$x^y =x ·(x^{y/2})^2$。
将这一过程递归下去,那我们可以仅进行${log(y)}$次乘方运算完成幂运算:
int FastPower(int x,int y){
long ans = 1;
while(y){
if(y&1){
ans *= x;
}
x *= x;
y = y>>1;
}
}
下面给出一个例子:$x = 3,y = 25 = 11001$
| 第i位 | ans | x *= x |
|---|---|---|
| 1 | $3$ | $3^2$ |
| 0 | $3$ | $3^4$ |
| 0 | $3$ | $3^8$ |
| 1 | $3·3^8$ | $3^{16}$ |
| 1 | $3·3^8·3^{16}$ | $3^{32}$ |
这就称为快速幂算法,那么接下来可以正式介绍快速幂取模运算了。
三、快速幂取模
快速幂取模,即给定整数x、y,N,求$x^ymodN$的运算。如果我们直接求出$x^y$再进行求模运算,很大可能会发生溢出,从而导致结果出错。
快速幂取模的思路来自:$ab\ modN \equiv (amodN)(bmodN)modN$
取a=b,则有$a^k\ modN \equiv (amodN)^kmodN$
则我们在进行快速幂的每一步运算之后,都可以加一次取模运算,这样得到的结果依然正确:
int FastPowerMod(int x,int y,int N){
long ans = 1;
while(y){
if(y&1){
ans = x*ans %N;
}
x = x*x %N;
y = y>>1;
}
}
同样给出一个例子:
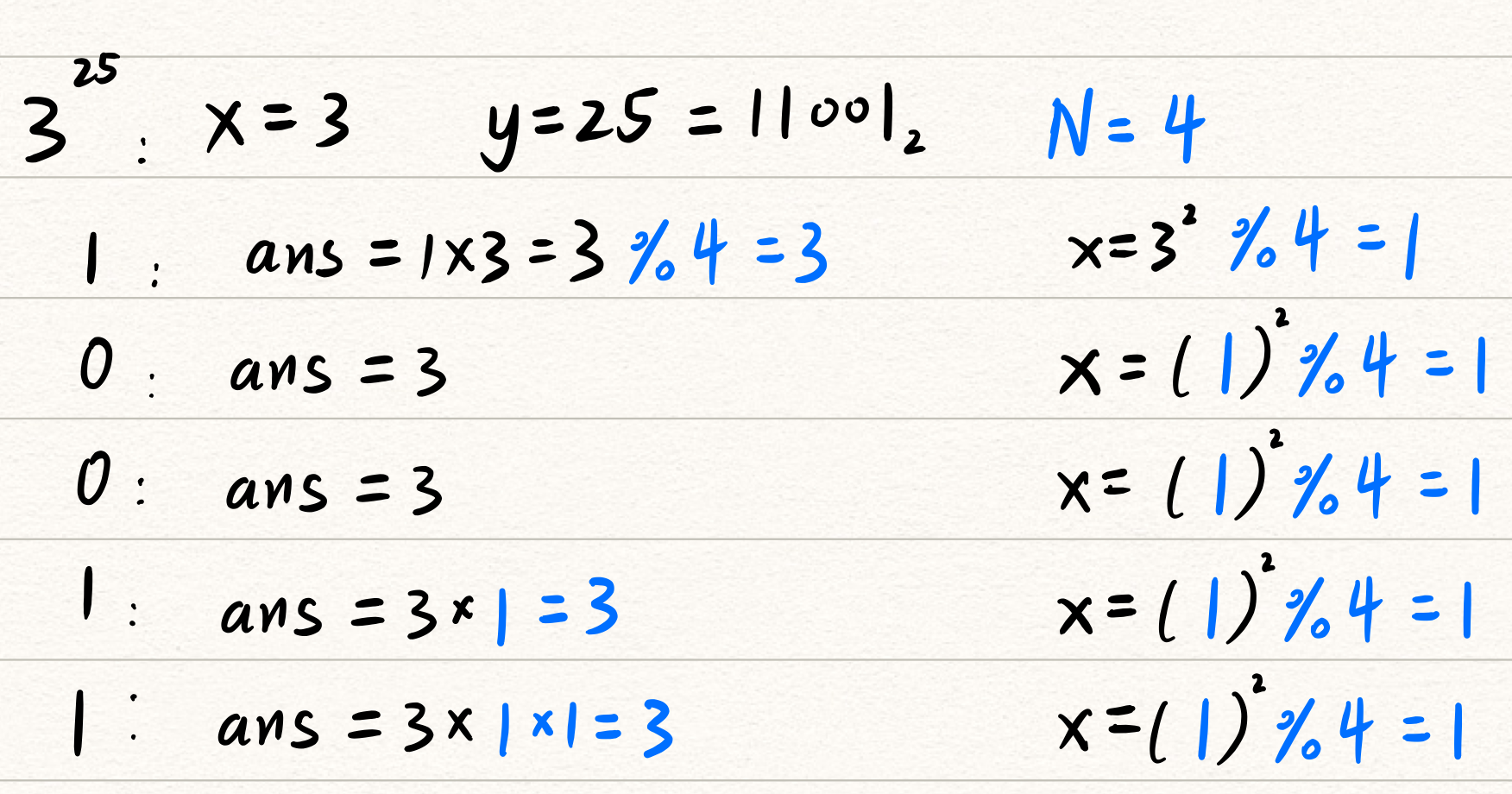
python实现如下:
x = int(input())
y = int(input())
N = int(input())
ans = 1
while y:
if y&1:
ans = x*ans %N;
x = x*x %N;
y = y>>1;
四、应用:素性测试
素性测试是检验一个给定的整数N是否为素数的测试。素性测试可以基于费马小定理进行:
若整数N为素数,则对$\forall a \in [1,N)$,$a^{N-1}\equiv 1 (modN)$
而且,如果N为合数,那么对绝大部分合数而言,至多只有一半的a满足,$a^{N-1}\equiv 1 (modN)$;但存在一类极其罕见的合数,称为Carmichael,针对所有与N互质的a,a都可以满足上述条件。
随机选择一个数N,可以通过以下步骤进行素性测试:
(1)随机选择一个数a<N,并且判断这个数a是否能被N整除,如果不能,重新选择。
(2)如果a^(N-1) % N != 1 ,那么直接退出循环,证明这个数不是素数;
(3)如果a^(N-1) % N != 1,那么这个数有可能是素数;
(4)多次选取a进行测试,如果均可通过素性测试,则判断N为素数。
在进行测试的过程中,求a^(N-1) % N这一步骤可以使用快速幂取模进行运算。
这种素性测试的结果不一定是正确的,只能通过多次选取a,提高准确率。米勒-拉宾素性测试是费马素性测试的改进方法,是当前运用最广泛的素性测试,且加上限制条件完全可以作为确定性算法。
五:应用:RSA公钥机制
RSA是一种公钥密码算法,被用于公钥密码和数字签名,它的明文、密钥和密文都是数字。RSA有一对用于加密的公钥(e,N),和一对用于解密的私钥(d,N),其解密原理如下:
1、密钥生成
- 找到一对素数P、Q;
- 取N = PQ
- $φ(N) = (P-1)(Q-1)$
- 得到公钥:取$e\in (1,φ(N))$,且$gcd(e,φ(N)) = 1$
- 得到私钥:求e mod φ(N)的逆d:$ed\equiv 1(modφ(N)) $
2、加密解密
对任意明文x,加密得到密文y:$y = x^e (modN)$
对密文y,解密得到明文x:$x = y^d (modN)$
对于密钥生成,可以使用素性测试取得P、Q,理论上PQ越大,密文的破译难度越高。对于加密和解密,发送方和接收方只需要使用快速幂算法,计算量较小。
RSA算法的安全性基于RSA问题的困难性,也就是基于大整数因子分解的困难性上。
RSA是非对称算法,加密和解密使用不同的密钥。