一、多项式计算
多项式创建
在Matlab中,n次多项式用一个n+1项的行向量表示,系数按照降幂排序。
例如,三元素向量
p = [4 2 3];
表示多项式$p(x)=4x^2+2x+3$
多项式计算
可以使用 polyval 函数根据特定值计算多项式。
例如使用 polyval 计算 p(3)。
polyval(p,3)
ans =
45
也可以使用 polyvalm 以矩阵方式计算多项式。也就是说变量x视为方阵X:
$p(x)=4X^2+2X+3I$
其中,X 是方阵,I 是单位矩阵。
X = [2 4 5; -1 0 3; 7 1 5];
polyvalm(p,X)
ans =
147 60 198
74 -1 46
206 134 265
我们用Horner方法自己编写一个计算多项式的函数:
function [ ans ] = horner( arr, x )
%输入行向量arr,变量x,求多项式结果p(x)
count = length(arr);
ans = arr(1);
for i=2:count
ans = ans*x +arr(i);
end
end
执行,得到结果和polyval相同:
>> polyval(p,3)
ans =
45
>> horner(p,3)
ans =
45
二、二次求根
已知二次根式$ax^2+bx+c=0$,求根公式为$(-b\pm\sqrt{b^2-4ac})/(2a)$,公式可化为$(-2c)/(b\pm \sqrt{b^2-4ac})$。

当$|b|≈\sqrt{b^2-4ac}$时,上述式子的分子或分母会变得极小,导致结果造成精度损失,所以,在进行运算时要选择计算相应公式,以减小误差:
- 当b>0,选择(1)的x2和(2)的x1;
- 当b<0,选择(1)的x1和(2)的x2;
同样,我们自己编写一个函数进行计算:
function [ x1 ,x2 ] = FindTheRoot( p )
%输入p = [a b c],求ax^2+bx+c=0的根x1,x2
a = p(1);
b = p(2);
c = p(3);
del = b^2-4*a*c;
x1 = NaN;
x2 = NaN;
if a==0 %一元一次方程
x1=-c/b;
x2=-c/b;
return
end
if del < 0 %根不存在
return
end
if b>0 %大于0
x1 = (-2*c)/(b+sqrt(del));
x2 = (-b-sqrt(del))/(2*a);
else %小于0
x1 = (-2*c)/(b-sqrt(del));
x2 = (-b+sqrt(del))/(2*a);
end
return
end
测试一下执行结果:
>> [a,b] = FindTheRoot([-1 -4 -2])
a =
-0.5858
b =
-3.4142
>> [a,b] = FindTheRoot([1 4 2])
a =
-0.5858
b =
-3.4142
三、不动点迭代
不动点指一个实数P,对函数g(x)满足P = g(P);通过点$p_0$开始,通过$p_{n+1} = g(p_n)$得到一个序列,这一过程称为不动点迭代。
不动点迭代可用于求解方程f(x) = 0,当然,并不是所有的f(x)都可以化为g(x)并求解,需要保证迭代收敛。迭代收敛性的判断不在这里进行说明,下面只给出不动点迭代的Matlab实现:
function [ p, k ,err ,P ] = fixpt( g ,p0 ,tole ,max1 )
%input:
%g:g(x)函数
%p0:第一个迭代点
%tole:允许的误差范围
%max1:最大迭代次数
%output:
%k:迭代次数
%p:所求结果
%err:绝对误差大小
%P:迭代序列
P(1) = p0;
for k = 2 : max1
p = feval(g,P(k-1));
P(k) = p;
err = abs(P(k) - P(k-1));
relerr = err/(abs(P(k))+eps);
if err<tole | relerr<tole
break;
end
end
if k == max1
disp("规定迭代次数内无法得到结果")
end
然后,我们编写一个函数fun1进行测试:
function y = fun1( x )
y = 1+0.5*sin(x);
end
这个函数与x = y的交点如图:plot(x,y,x,z,'-.')
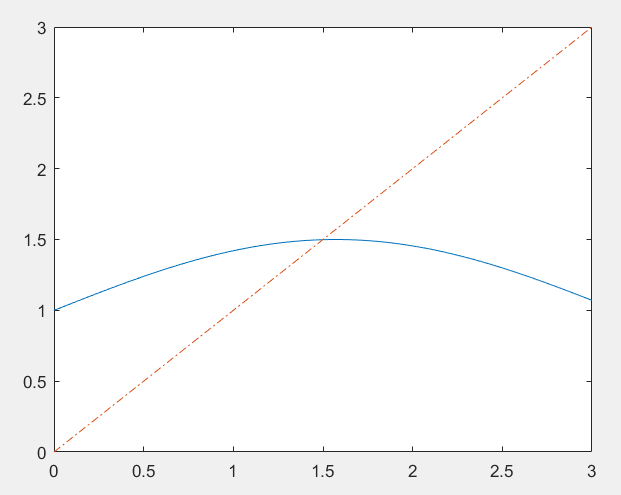
利用不动点迭代求解,得到结果如下:
>> [ p, k ,err ,P ] =fixpt('fun1',-1,0.000001,10000)
p =
1.4987
k =
8
err =
1.0668e-06
P =
-1.0000 0.5793 1.2737 1.4781
1.4979 1.4987 1.4987 1.4987
四、二分法求根
对连续函数f(x),给定一个区间[a,b],其中f(a)f(b)<0,通过不断二分求函数的根:
function [ c, err ,yc ] = bisect( f ,a ,b ,tole )
%input:
%f:f(x)函数
%a、b:区间
%tole:允许的误差大小
%output:
%c:根
%err:绝对误差大小
%yc:f(c)
ya = feval(f,a);
yb = feval(f,b);
if ya*yb>0
disp("不满足f(a)f(b)<0");
return
end
max1 = 1+(log(b-1)-log(tole))/(log(2));
%终止条件1:最大迭代次数
for k = 1:max1
c = (a+b)/2;
yc = feval(f,c);
if yc== 0
err = 0
return
end
if yb*yc>0
b = c;
yb = yc;
else
a = c;
ya = yc;
end
if b-a<tole %终止条件2:ab区间大小
break
end
end
c = (a+b)/2;
err = abs(b-a);
yc = feval(f,c);
end
同样,编写函数fun1 = x^3,,执行:
>> [ c, err ,yc ] = bisect( 'fun1' ,-2 ,1 ,0.001 )
c =
-1.2207e-04
err =
7.3242e-04
yc =
-1.8190e-12
>> [ c, err ,yc ] = bisect( 'fun1' ,-2 ,2 ,0.001 )
err =
0
c =
0
err =
0
yc =
0
五、试值法求根
对连续函数f(x),给定一个区间[a,b],其中f(a)f(b)<0,通过取(a,f(a))与(b,f(b))的连线与x轴交点(c,0),得到序列c,用c拟合f(x)=0的根:
function [ c, err ,yc ] = regula( f ,a ,b ,tole,epsilon,max1 )
%input:
%f:f(x)函数
%a、b:区间
%tole:c误差大小
%epsilon:f(c)误差大小
%max1:最大迭代次数
%output:
%c:根
%err:绝对误差大小
%yc:f(c)
ya = feval(f,a);
yb = feval(f,b);
c = NaN;
err = NaN;
yc = NaN;
if ya*yb>0
disp("不满足f(a)f(b)<0");
return
end
for k = 1:max1 %最大迭代次数作为终止条件
bc = yb*(b-a)/(yb-ya);
c = b-bc;
ac = c-a;
yc = feval(f,c);
if yc== 0
err = 0
return
end
if yb*yc>0
b = c;
yb = yc;
else
a = c;
ya = yc;
end
dx = min(ac,bc);%c离a、b的距离最小值
if dx<tole
err = abs(b-a)/2;
return
end %x轴区间作为终止条件
if abs(yc)<epsilon
err = abs(b-a)/2;
return
end %y轴区间作为终止条件
end
err = abs(b-a)/2;
yc = feval(f,c);
end
与二分法使用同一函数测例:
>> [ c, err ,yc ] = regula( 'fun1' ,-2 ,1 ,0.001 ,0.001,10000)
c =
0.1529
err =
1.0765
yc =
0.0036
>> [ c, err ,yc ] = regula( 'fun1' ,-2 ,2 ,0.001 ,0.001,10000)
err =
0
c =
0
err =
0
yc =
0
六、求解近似根位置
为了粗略估计根在区间中的位置,使用等距采样点将区间分成n个小区间,判断每个区间是否满足根存在的条件:
function R = approot (f,X,epsilon)
%Input
%f:输入函数
%X:等距采样点序列x
%epsilon:y的误差
%Output
%R:近似根序列
n=length(X);
for i=1:n
Y(i) = feval(f,X(i));
end
yrange = max(Y)-min(Y);
epsilon2 = yrange*epsilon;
m=0;%近似根数量
X(n+1)=X(n);%防止溢出
Y(n+1)=Y(n);
for k=2:n
if Y(k-1)*Y(k)<=0 %根存在条件1
m=m+1;
R(m)=(X(k-1)+X(k))/2;
end
s=(Y(k)-Y(k-1))*(Y(k+1)-Y(k));
if (abs(Y(k)) < epsilon2) & (s<=0) %根存在条件2
m=m+1;
R(m)=X(k);
end
end
测试函数:
>> R = approot ('sin',X,0.00001)
R =
0.0005 3.1415 6.2835 9.4245
七、牛顿-拉弗森迭代
牛顿法只需要函数f和f的导数,且给定一个起始点,即可开始计算。
function [p0, err, k, y] = newton( f, df, p0, delta, eps, max1 )
%Input
%f:输入函数
%df: f的导数
%p0:初始点
%eps:y的误差范围
%delta:p0的误差范围
%max1:最大迭代次数
%Output
%p0:最终结果
%err:最终误差
%k:迭代次数
%y:f(p0)
for k = 1 : max1
p1 = p0 - feval(f,p0)/feval(df,p0);
err = abs(p1-p0);
p0 = p1;
y = feval(f,p0);
if (err<delta)|(abs(y)<eps)
break;
end
end
end
所用的函数:
function y = f( x )
y = x^3 - 3*x + 2;
end
function y = df( x )
y = 3*x^2 - 3;
end
测试(从p0 = 1.2开始):
>> [p0, err, k, y] = newton('f','df',1.2,0.000000000001,0.0000000001,100)
p0 =
1.0000
err =
3.2510e-06
k =
16
y =
3.1708e-11
八、割线法
割线法不必计算f的导数,但是需要两个起始点p0、p1,求割线进行迭代。
function [p1, err, k, y] = secant( f, p0, p1, delta, eps, max1 )
%Input
%f:输入函数
%p0、p1:初始点
%eps:y的误差范围
%delta:p0的误差范围
%max1:最大迭代次数
%Output
%p1:最终结果
%err:最终误差
%k:迭代次数
%y:f(p0)
for k = 1 : max1
y0 = feval(f,p0);
y1 = feval(f,p1);
p2 = p1 - y1*(p1-p0)/(y1 - y0);
err = abs(p2-p1);
p0 = p1;
p1 = p2;
y = feval(f,p1);
if (err<delta)|(abs(y)<eps)
break;
end
end
end
所用的函数和牛顿法相同,进行测试(从p0 = 1.2开始):
[p1, err, k, y] = secant('f',1.2,1.21, 0.000000000001,0.0000000001,100)
p1 =
1.0000
err =
2.9315e-06
k =
22
y =
6.7494e-11