一、简介
卡尔曼滤波:在含有不确定信息的动态系统中,得到对系统状态的最佳估计。
简单来说,就是根据当前时刻的测量值以及上一时刻的预测值以及误差,来计算得到当前时刻的最佳预测值。
二、处理过程
用一个简单的例子说明卡尔曼滤波的一般处理过程,并得到计算公式:
1、预测状态量
假设我们要研究一辆汽车的行驶状态,对一个行驶状态来说,我们需要两个状态量;位移l、速度v;同时,可以有控制量对状态量进行影响,这里引入一个控制量:加速度a。
在不考虑外部影响的情况下,预测的状态量可以表示为:

两个状态量之间的关系用协方差矩阵表示:
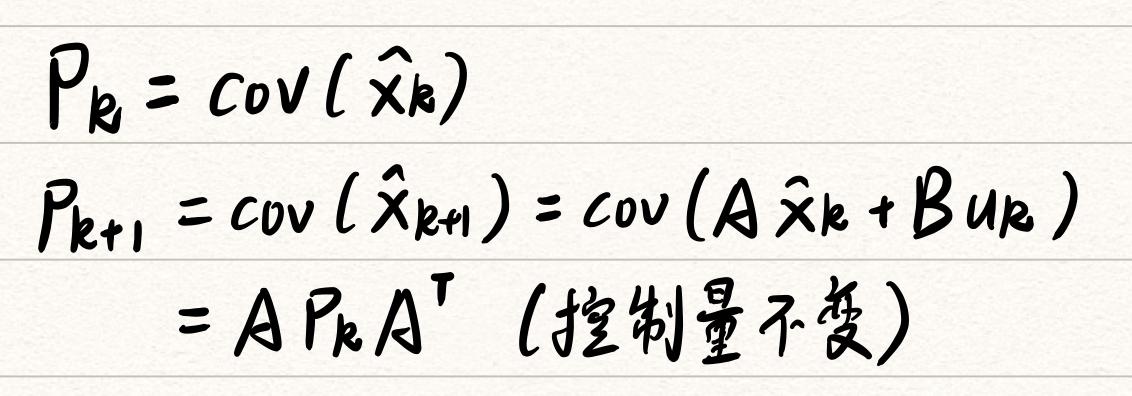
接下来我们考虑外部影响,假设外部对系统影响的噪声为$w_k$ ,噪声满足高斯分布,协方差矩阵为Q ,修改上述公式:

上面的方程称为状态预测方程和协方差预测方程。
2、测量状态量
上面是通过上一时刻状态预测当前时刻状态,但这种预测往往是粗略和不精准的。实际上,汽车一般还装有传感器(GPS、电子陀螺和里程仪等)来测量汽车的当前状态:位置和速度。从传感器的测量数据中,我们大致能猜到系统当前处于什么状态,但仍存在不确定性。
那么,我们需要综合当前时刻测量值和根据上一时刻得到的估计值,得到最终的估计值。
传感器读取的数据单位/尺度有可能与我们跟踪状态的单位/尺度不一样,引入一个矩阵H,将上面预测的状态量映射到传感器测量的空间。可以得到此时的预测状态量的均值$\mu _p$和相对应的协方差:

可以发现,预测值$z_1$满足高斯分布;
同时,我们假设测量值$z_2$也满足高斯分布,其中$\mu _m$为测量状态量的均值,$R$为描述传感器测量噪声对应状态量的协方差:

现在我们有了两个高斯分布,一个是在预测值附近,一个是在传感器读数附近。 我们最终需要在两个高斯分布中找到一个最优解。
3、数据融合
将两个高斯分布的数据进行整合,这一操作即为数据融合。实际上,数据融合只进行了一个简单的操作——将两个高斯分布相乘,得到一个新的高斯分布。接下来我们分析新的高斯分布与原高斯分布的联系:
设两个一维高斯分布X、Y,将其概率分布函数相乘得到新的分布
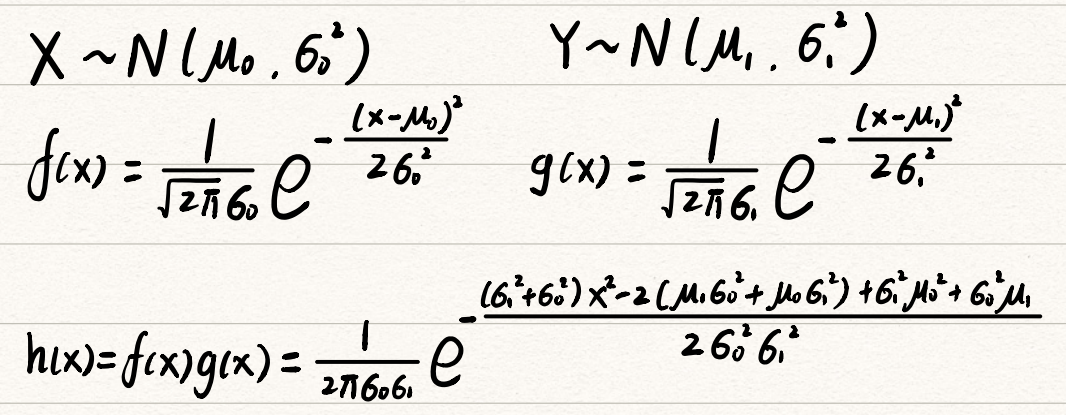
将新的概率分布函数进行整理,可以得到新的均值与方差,并引入K化简
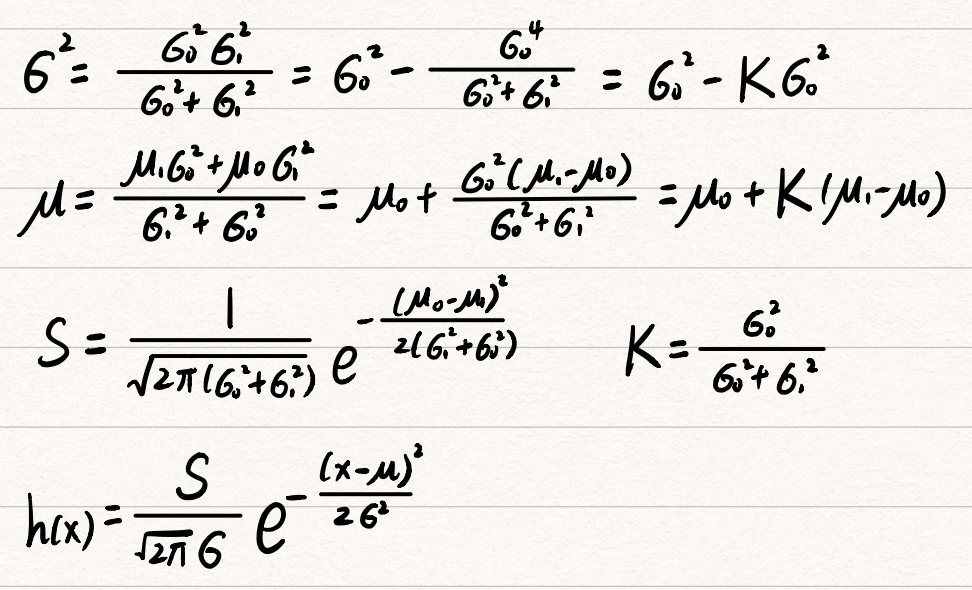
可以得到新的分布Z仍满足高斯分布,与原高斯分布的关系如表达式。
将预测值$z_1$和测量值$z_2$两个高斯分布进行数据融合,得到最终的高斯分布Z,其中K为卡尔曼增益,是估计量的方差占总方差(估计量方差和测量方差)的比重:
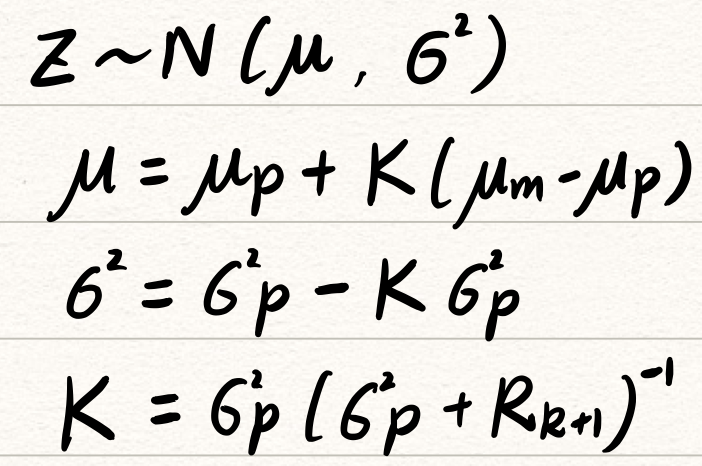
将上述$K,\mu , \sigma$整理出来,得到最终的$x’{k+1}$和$P’{k+1}$(注意单位的映射)

将上面的式子进行化简,得到卡尔曼滤波的核心公式(后验):
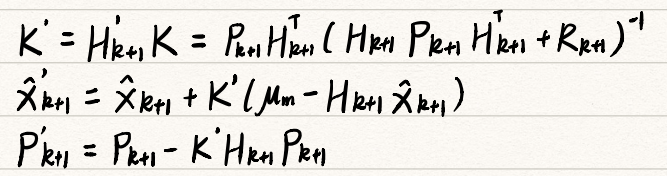
其中$x_{k+1}$和$P_{k+1}$由以下式子得出(先验):
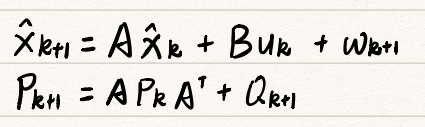
三、OpenCV中的卡尔曼滤波
OpenCV的卡尔曼滤波定义在KalmanFilter类中,类声明的所在文件为\opencv-4.0.0\modules\video\include\opencv2\video\tracking.hpp。
class CV_EXPORTS_W KalmanFilter
{
public:
CV_WRAP KalmanFilter();
/*
默认构造函数
@param dynamParams Dimensionality of the state.
@param measureParams Dimensionality of the measurement.
@param controlParams Dimensionality of the control vector.
@param type Type of the created matrices that should be CV_32F or CV_64F.
*/
CV_WRAP KalmanFilter( int dynamParams, int measureParams, int controlParams = 0, int type = CV_32F );
/*
构造函数
@param dynamParams Dimensionality of the state.
@param measureParams Dimensionality of the measurement.
@param controlParams Dimensionality of the control vector.
@param type Type of the created matrices that should be CV_32F or CV_64F.
*/
void init( int dynamParams, int measureParams, int controlParams = 0, int type = CV_32F );
/** @brief Computes a predicted state.
初始化对象
@param control The optional input control
*/
CV_WRAP const Mat& predict( const Mat& control = Mat() );
/** @brief Updates the predicted state from the measurement.
计算预测状态量
@param measurement The measured system parameters
*/
CV_WRAP const Mat& correct( const Mat& measurement );
//根据测量值更新状态值
CV_PROP_RW Mat statePre; //!< predicted state (x'(k)): x(k)=A*x(k-1)+B*u(k)
CV_PROP_RW Mat statePost; //!< corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
CV_PROP_RW Mat transitionMatrix; //!< state transition matrix (A)
CV_PROP_RW Mat controlMatrix; //!< control matrix (B) (not used if there is no control)
CV_PROP_RW Mat measurementMatrix; //!< measurement matrix (H)
CV_PROP_RW Mat processNoiseCov; //!< process noise covariance matrix (Q)
CV_PROP_RW Mat measurementNoiseCov;//!< measurement noise covariance matrix (R)
CV_PROP_RW Mat errorCovPre; //!< priori error estimate covariance matrix (P'(k)): P'(k)=A*P(k-1)*At + Q)*/
CV_PROP_RW Mat gain; //!< Kalman gain matrix (K(k)): K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)
CV_PROP_RW Mat errorCovPost; //!< posteriori error estimate covariance matrix (P(k)): P(k)=(I-K(k)*H)*P'(k)
// temporary matrices
Mat temp1;
Mat temp2;
Mat temp3;
Mat temp4;
Mat temp5;
};
成员函数的定义位于\opencv-4.0.0\modules\video\src\kalman.cpp中:
KalmanFilter::KalmanFilter(int dynamParams, int measureParams, int controlParams, int type)
{
init(dynamParams, measureParams, controlParams, type);
}
void KalmanFilter::init(int DP, int MP, int CP, int type)
{
CV_Assert( DP > 0 && MP > 0 );
CV_Assert( type == CV_32F || type == CV_64F );
CP = std::max(CP, 0);
//矩阵初始化
statePre = Mat::zeros(DP, 1, type);
statePost = Mat::zeros(DP, 1, type);
transitionMatrix = Mat::eye(DP, DP, type);
processNoiseCov = Mat::eye(DP, DP, type);
measurementMatrix = Mat::zeros(MP, DP, type);
measurementNoiseCov = Mat::eye(MP, MP, type);
errorCovPre = Mat::zeros(DP, DP, type);
errorCovPost = Mat::zeros(DP, DP, type);
gain = Mat::zeros(DP, MP, type);
if( CP > 0 )
controlMatrix = Mat::zeros(DP, CP, type);
else
controlMatrix.release();
temp1.create(DP, DP, type);
temp2.create(MP, DP, type);
temp3.create(MP, MP, type);
temp4.create(MP, DP, type);
temp5.create(MP, 1, type);
}
const Mat& KalmanFilter::predict(const Mat& control)
{
CV_INSTRUMENT_REGION();
// update the state: x'(k) = A*x(k)
statePre = transitionMatrix*statePost;
if( !control.empty() )
// x'(k) = x'(k) + B*u(k)
statePre += controlMatrix*control;
// update error covariance matrices: temp1 = A*P(k)
temp1 = transitionMatrix*errorCovPost;
// P'(k) = temp1*At + Q
gemm(temp1, transitionMatrix, 1, processNoiseCov, 1, errorCovPre, GEMM_2_T);
// handle the case when there will be measurement before the next predict.
statePre.copyTo(statePost);
errorCovPre.copyTo(errorCovPost);
return statePre;
}
const Mat& KalmanFilter::correct(const Mat& measurement)
{
CV_INSTRUMENT_REGION();
// temp2 = H*P'(k)
temp2 = measurementMatrix * errorCovPre;
// temp3 = temp2*Ht + R
gemm(temp2, measurementMatrix, 1, measurementNoiseCov, 1, temp3, GEMM_2_T);
// temp4 = inv(temp3)*temp2 = Kt(k)
solve(temp3, temp2, temp4, DECOMP_SVD);
// K(k)
gain = temp4.t();
// temp5 = z(k) - H*x'(k)
temp5 = measurement - measurementMatrix*statePre;
// x(k) = x'(k) + K(k)*temp5
statePost = statePre + gain*temp5;
// P(k) = P'(k) - K(k)*temp2
errorCovPost = errorCovPre - gain*temp2;
return statePost;
}
KalmanFilter类包含十个成员变量,构造函数需要定义状态量、观测量、控制量的维数;
初始化时需要给定三个初始状态:前一时刻状态量x、协方差矩阵P、观测值y,和五个参数:A、B、H、Q、R;
predict函数用于计算先验估计值和先验协方差矩阵,输入参数为控制量;
correct函数用于计算卡尔曼增益、最终估计结果、后验状态量、后验协方差矩阵,输入参数为观测值;